《まとめ解説》磁性材料に関する単位がこれで分かる!
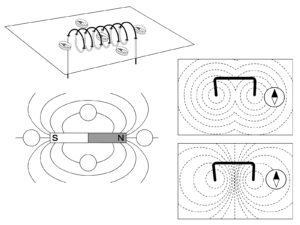
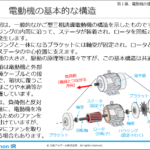
今回は、磁性材料そのものではなく、磁性材料に関連するMKSA単位を取り上げます。
Wb(ウェーバ)、T(テスラ)など単位量に固有の名称である単位名称、および単位名称と基本単位を組み合わせた実用的な物理単位を紹介します。
目次
1.真空の透磁率:μ0
はじめに真空の透磁率を紹介します。
電流の単位アンペアを追加したMKSA単位が提案された際、真空の透磁率μ0の値と単位が下記のように設定されました。
μ0:真空の透磁率 4π×10-7 [H/m]または[N/A2]
μ0の物理単位 [H/m] のH(ヘンリー)は、コイルに印加する電流I[A]と、発生する磁束Φ[Wb]との関係式である、Φ=LI のインダクタンスLの単位名称です。インダクタンスLの物理単位は [Wb/A] ですので、今後μ0の物理単位は [Wb/Am] または [N/A2] と書き換えます。
ここで、真空の透磁率μ0の値、4π×10-7 を導出します。
(a)電流の大きさの定義
図1に示す一方の平行導線に電流を流すと、「ビオ・サバールの法則」(※注記1)により、他方の導線の位置に磁束密度が発生します。
そして電流が流れている他方の導線には「ローレンツ力」(※注記2)、「アンペールの力」(※注記3)が作用します。
具体的には、無限長の平行導線に等しい大きさの電流Iを流し、1[m]の距離を離して置いたときに、互いの導線の長さ1[m]あたりに作用する力Fが2×10-7[N]となる時、この電流Iの大きさを1[A]と定義します。

[図1.電流の定義]
(b)磁束密度の大きさの定義
図2に示す磁束密度の空間に置かれた電流(電流素片)には、「ローレンツ力」と「アンペールの力」が作用します。
具体的には、1[Wb/m2]の磁束密度Bの大きさは、磁束密度Bに直交する1[Am]の電流素片に1[N]の力Fが作用する大きさと定義します。

[図2.磁束密度の定義]
(c)「ビオ・サバールの法則」
直線電流I[A]からr[m]離れた位置の磁束密度B[Wb/m2]は、式(1)となります。
B=μ0I/2πr ・・・(1)
上記(a)(b)から平行導線に1[A]の電流を流し、1[m]の距離を離して置いたときに互いの導線に作用する力Fは導線1[m]あたり 2×10-7[N] になり、その導線の位置の磁束密度Bは 2×10-7[Wb/m2] になります。
この直線電流1[A]、距離1[m]、磁束密度:2×10-7[Wb/m2]の関係を上記(c)の式(1)
B=μ0I/2πr に代入すると、真空の透磁率μ0の値は下記のように導出されます。
μ0=2πB/I
=2π・2×10-7/I
=4π×10-7
なお、真空の透磁率μ0の物理単位は、[Wb/Am]または[N/A2]です。
※注記1:「ビオ・サバールの法則」
定常電流素片IdsがP点に作る磁束密度dBは、
dB=μ0/4π・Ids×er/r2 ・・・(2)
また磁場dHは、
dH=1/4π・Ids×er/r2 ・・・(3)
ここで、μ0は真空の透磁率、rは電流素片とP点の距離、erは単位ベクトル です。
式(2)において、直線電流の-∞から+∞の位置にある電流素片が作る磁束密度を積分すると、図3の直線電流から距離a[m]のP点の磁束密度Bは式(4)となります。
B=μ0I/2πa ・・・(4)
ここで、μ0:真空の透磁率(4π×10-7)[Wb/Am]または[N/A2]、I:電流[A]、a:直線電流からの距離[m]、また図3の直線電流から距離a[m]のP点の磁場Hは、式(5)となります。
H=I/2πa ・・・(5)
ここで、I:電流[A]、a:直線電流からの距離[m] です。
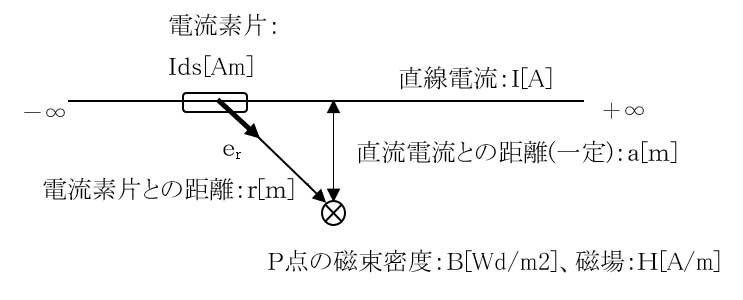
[図3.ビオ・サバールの法則]
※注記2:「ローレンツ力」
運動する電荷に作用する力は、式(6)に示すように磁束密度と電荷の速度の外積と電荷の大きさの積になります。この力が「ローレンツ力」です。
F=qv×B ・・・(6)
ここで、F:「ローレンツ力」[N]、q:電荷[c]、v:電荷の速度[m/s]、B:磁束密度[Wb/m2] です。
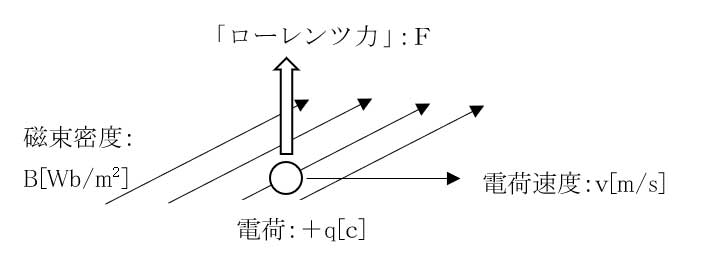
[図4.ローレンツ力]
※注記3:「アンペールの力」
電荷q、速度vの電子1個に対する「ローレンツ力」は、式(6)より F=qvB となります。
電子密度n[/m3]、断面積S[m2]、長さL[m]の導線に作用する力は、導線中の電子数nSLを式(6)に乗じて F=qvBnSL となります。
電流は断面を1秒間に通過する電子の電荷(I[A]=q[c]v[m/s]n[/m3]S[m2])ですので、式(6)から図5の電流が流れる導線に作用する力Fは式(7)となります。
F=IBL ・・・(7)
ここで、F:「アンペールの力」[N]、B:磁束密度[Wb/m2]、I:電流[A]、L:導線長さ[m] です。
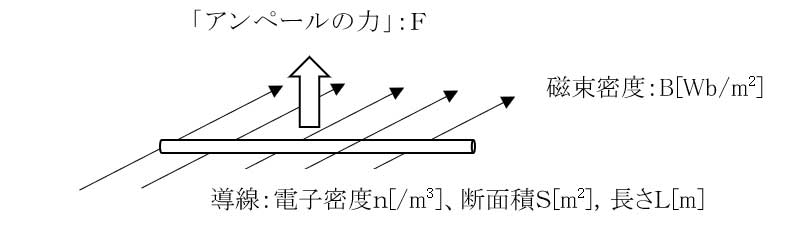
[図5.アンペールの力]
2.磁性材料に関連する単位
つぎに「磁気のクーロンの法則」をもとにして、磁性材料に関連する単位を紹介します。
(1)磁気のクーロンの法則
単極磁荷の存在を仮定して、磁荷 qm1と磁荷qm2の間に作用する力を示す「磁気のクーロンの法則」を式(8)に示します。
F=qm1qm2/(4πμ0r2) ・・・(8)
F:磁荷qm1と磁荷qm2の間に作用する力[N] qm1、qm2:磁荷[Wb] μ0:真空の透磁率(4π×10-7)[Wb/Am]または[N/A2] r:磁荷qm1と磁荷qm2の距離[m]
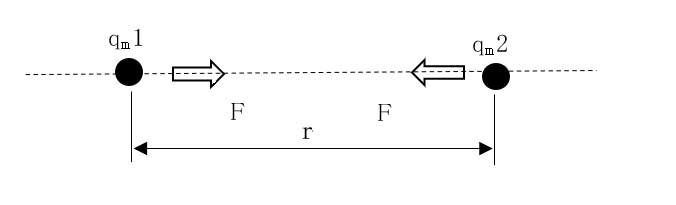
[図6.磁気のクーロンの法則]
(2)磁荷:qm
磁荷は磁極の存在を仮定したときに、磁極が帯びている磁気の量です。
磁荷のほかに磁気量、磁極の強さとも呼び、N極の磁荷は正、S極の磁荷は負と定義します。
「磁気のクーロンの法則」において、図6に示される磁荷qm1と磁荷qm2が同じ大きさで、真空中の1[m]離れた磁荷の間に作用する力が 6.33×104[N] である場合、その磁荷の大きさを1[Wb(ウェーバ)]と定義しています。
磁荷:qmの単位名称は [Wb(ウェーバ)]、また物理単位は「磁気のクーロンの法則」式(8)より、
qm1qm2=F×(4πμ0r2) ですので、([N][N/A2] [m2])1/2 => [Nm/A]となります。

[図7.磁荷の大きさの定義]
(3)磁場:H
磁場は、磁気力が作用する空間の各点における、大きさと向きを持つベクトルです。
磁荷が受ける力の大きさは、式(9)に示すように、磁場と磁荷の大きさに比例します。
磁場Hの大きさと向きは、図8に示すように、1[Wb]のN極の磁荷qm1を置いたときに磁荷qm1が受ける力と同じ大きさ、同じ向きとなります。
F=qm1H ・・・(9)
また、「磁気のクーロンの法則」の式(8)より
H=qm2/(4πμ0r2) ・・・(10)
ここで、
F:磁荷qmに作用する力[N]
qm:磁荷qmの大きさ[Nm/A]
μ0:真空の透磁率(4π×10-7)[N/A2]
磁場:Hの物理単位は式(10)より、[Nm/A]/[N/A2][m2] => [A/m] となります。
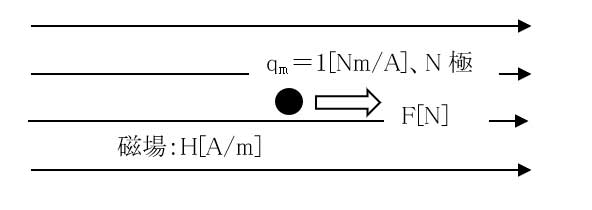
[図8.磁場]
また、磁場はまた前出の注記1「ビオ・サバールの法則」により、電流と関係があります。
直流電流から生じる磁場の強さは、電流に比例し電流を中心とした半径aの円周の長さ(磁力線の長さ)に反比例します。
直流電流の場合、電流:I[A]が半径:a[m]の円周に沿ってつくる磁場:Hは、式(5)でした。
H=I/2πa ・・・(5)
ここで、I:電流[A]、a:直線電流からの距離[m] 式(5)から磁場:Hの物理単位は、[A]/[m] => [A/m]となります。
(4)磁気双極子モーメント:m
正負の磁極の対を「磁気双極子」とよび、単独の磁極の存在は現時点では確認されていないので、磁気の基本的な要素は磁気双極子となります。
磁気双極子モーメントmは、図9に示すように、磁荷の大きさqm、正負の磁極間の距離dの場合、式(11)に示す大きさqmd、向きはS局からN極方向のベクトルになります。
m=qmd ・・・(11)
ここで
qm:磁荷qmの大きさ[Wb]または[Nm/A]
d:正負の磁極間の距離[m]
磁気双極子モーメント:mの物理単位は式(11)より [Wbm]または[Nm2/A]となります。
ただし現実には磁荷という物理量は存在しないので、qmdと等価な回転を与えるモーメントを「磁気双極子モーメント」と呼びます。
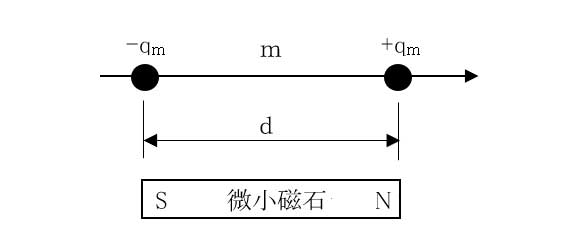
[図9.磁気双極子モーメント]
(5)体積磁化:M
物質に磁場が作用して仮想的に物質の表面に磁極が生じたとき、その物質は磁化されます。
磁極の磁荷により、磁極表面の法線方向に、単位面積当たりMの磁化が発生します。
その大きさは、磁気双極子モーメントのベクトル和の単位体積当たりの値で定義されます。
図10は磁性体の磁気双極子モーメントmが一方向に揃っているケースを示しています。
M =Σm/体積 ・・・(12)
体積磁化:Mの物理単位は、式(12)に示すように物理単位が[Wbm]の磁気双極子モーメント:mを体積[m3]で除して、 [Wb/m2]となります。
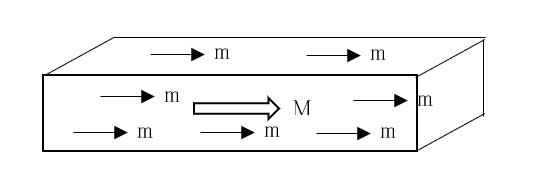
[図10.体積磁化]
(6)磁束:Φ
磁束線は空間内の物質の透磁率に関係なく、1[Wb]の磁荷から1本発生します。
図11の例は、qm=5[Wb]の大きさの磁荷から5本の磁束線が発生しています。
磁束は、磁束線の本数を表すスカラーで、方向は持ちません。
磁束:Φの単位名称は磁荷と同じ[Wb(ウェーバ)]、物理単位は本数ではなく磁荷:qmと同じ[Nm/A]となります。
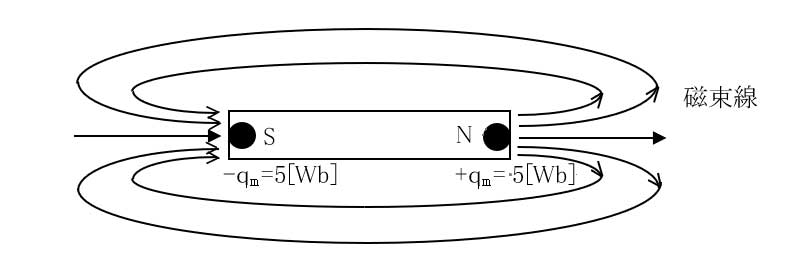
[図11.磁束]
(7)磁束密度:B
磁束線の方向に垂直な単位面積1[m2]当たりの磁束が磁束密度Bの大きさです。
磁束密度Bはベクトルで、真空中では、B=μ0Hの関係があります。
B=Φ/面積 ・・・(13)
図12の場合、磁束密度Bの大きさと向きは、位置aで約3[Wb/m2]右方向、位置bで約2[Wb/m2]左方向、位置cで約5[Wb/m2]右方向となります。
磁束:Φの単位名称が[Wb]、物理単位が[Nm/A]ですので、式(13)から磁束密度:Bの物理単位は[Wb/m2]または[N/Am]となります。
また、磁束密度:Bの単位名称は[T(テスラ)]です。

[図12.磁束密度]
また、前出の注記2「ローレンツ力」式(6)に示すように、運動する電荷は磁束密度と電荷の速度の外積と電荷量の積の力を受けます。
F=qv×B ・・・(6)
ここで、F:「ローレンツ力」[N]、q:電荷量[c]、v:電荷の速度[m/s]、
磁束密度:Bの物理単位は、式(6)より[N/c(m/s)] => [N/m(c/s)] => [N/Am]となります。
(8)最大エネルギ積:(BH)max
磁性材料の磁気エネルギを蓄える性能は、永久磁石の強さに相当します。
磁性材料の磁化曲線において、図12のヒステリシス曲線の第2象限の一点から磁場:H軸と磁束密度:B軸へ垂線を引いてできる長方形の面積を「エネルギ積」と呼びBHで表します。
そして、減磁曲線上で最大となる図13の点Qのエネルギ積を「最大エネルギ積」と呼び(BH)max で表します。
(BH)max=BH ・・・(14)
最大エネルギ積:(BH)maxの物理単位は式(14)より、
[A/m][N/mA] => [N/m2] => [Nm/m3] => [J/m3]となります。
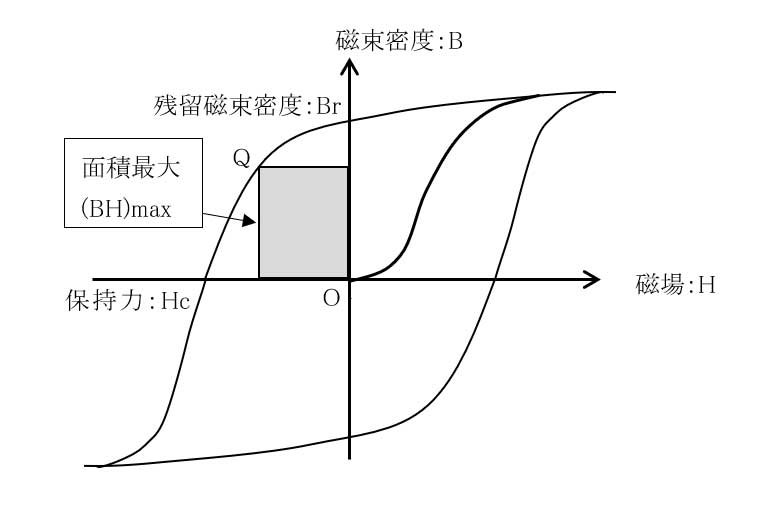
[図13.(BH)max]
3.磁性材料に関する単位のまとめ
磁性材料に関連する単位は、電流および透磁率の設定と定量化が先行した経緯があるようです。
今回のMKSA単位の紹介も、はじめに電流と磁気と力の関係を明らかにした「ビオ・サバールの法則」「ローレンツ力」「アンペールの力」から真空の透磁率を導出し、次に磁荷を基本量とした「磁気のクーロンの法則」をもとにして、磁性材料に関連する単位を紹介しました。
磁場と磁束密度については、磁性材料の性質と関係した(その1)と、電流との関係から展開した(その2)を併記しました。紹介しました磁性材料に関連する単位を表1に示します。
表1には、単位名称、物理単位に加え、長さ(m)、質量(Kg)、時間(s)、電流(A)の基本単位からなるMKSA組立単位も記載しましたので、物理量の関係を考える際の参考にしてください。
| 物理量名称 | 記号 | 単位名称 | 物理単位 | 組立単位 | |||
| M(m) | K(kg) | S(s) | A(A) | ||||
| 力 | F | N(ニュートン) | J/m、kgm/s2 | 1 | 1 | -2 | 0 |
| エネルギ | U | J(ジュール) | Nm | 2 | 1 | -2 | 0 |
| インダクタンス | L | H(ヘンリー) | J/A2、Wb/A | 2 | 1 | -2 | -2 |
| 透磁率 | μ | H/m、N/A2 | 1 | 1 | -2 | -2 | |
| 磁荷 | qm | Wb(ウェーバ) | Nm/A、Vs | 2 | 1 | -2 | -1 |
| 磁気双極子モーメント | m | Wbm、Nm2/A | 3 | 1 | -2 | -1 | |
| 体積磁化 | M | Wb/m2 | 0 | 1 | -2 | 1 | |
| 磁束 | Φ | Wb(ウェーバ) | Nm/A、Vs | 2 | 1 | -2 | -1 |
| 磁束密度 | B | T(テスラ) | Wb/m2、N/Am | 0 | 1 | -2 | -1 |
| 最大エネルギ積 | (BH)max | J/m3 | -1 | 1 | -2 | 0 | |
[表1.磁性材料に関連する単位]
(日本アイアール株式会社 特許調査部 Y・O)