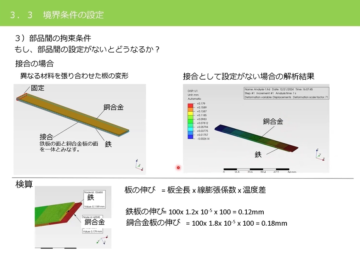
【機械設計マスターへの道】衝撃荷重と材料の強度を考える（衝撃応力の計算、シャルピー衝撃試験）

Tweet

Pocket

今回は、物体が落下して他の物体に衝突するときなどのように、極短時間に加わる「衝撃荷重」によって生じる衝撃応力と材料の強度について考えてみたいと思います。

１．ひずみエネルギー、最大弾性ひずみエネルギー

断面一様の棒に引張荷重Wを加えたときの棒の伸びをλとします。
ある限界の荷重（弾性限度）まではWとλは比例関係にあり、荷重Wをゼロにすれば伸びλもゼロとなって元に戻ります。弾性限度内でWをわずかに増加したときの棒の伸び量増分をdλとすれば、荷重増加は棒に対してWdλの仕事をしたことになります。
この仕事分は、荷重増加分がなくなったときに元に戻ろうとする内部エネルギーとして棒に蓄えられます。
これをひずみエネルギーUといいます。

荷重ゼロから弾性限度内の任意の伸びλに至るまでに蓄えられるひずみエネルギーは、

　　　・・・（1）

棒の断面積A、長さℓ、ヤング率をE、荷重Wによって生じる引張応力をσ、ひずみをεとすれば、
W=Aσ、λ=ℓε、ε=σ/E の関係があるので、（1）式は、

　　　・・・（2）

となります。

また、(2)式を、棒の体積Aℓで割れば、単位体積当たりのひずみエネルギーuは

　u=σ²/2E　　・・・（3）

となります。

棒の材料の弾性限度における応力をσ_eとしたとき u_e=σ_e²/2E を、最大弾性ひずみエネルギーといいます。

最大弾性ひずみエネルギーu_eは、衝撃荷重に対する材料の強さ（抵抗力）を考えるときに重要な指標となります。u_eが大きい材料ほど衝撃荷重による破壊に至るまでに、より多くのエネルギーを吸収できることになりますから、衝撃に対してより安全であるということができます。

２．衝撃応力

図のように上端を固定した長さℓ、断面積Aの棒の先端に円板をつけて、棒に挿入した質量M[kg]の錘を高さh[m]から落下させて円板に衝突させて棒に衝撃荷重を与えたとき、棒に生ずる衝撃応力σについて考えます。

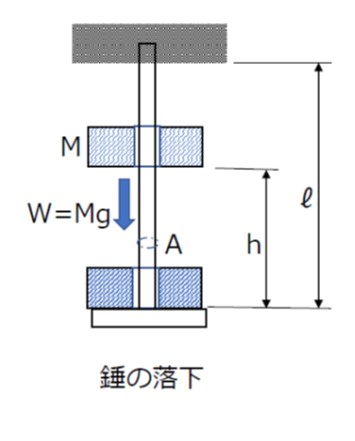
重力加速度をgとすれば、錘が落下するときの静荷重は、W=Mg となります。
錘が落下して円板に衝突したときに生じる棒の伸びをλとすれば、衝突により棒に与えられるエネルギーは　W(h+λ) [N-m]　となります。（gは重力加速度）

このエネルギーがすべて、ひずみエネルギーとして棒に蓄えられるとすれば、（2）式より

　Aℓσ²/2E = W(h+λ)　　・・・（4）

伸びλ、長さℓ、応力σ、ヤング率Eの間には、λ=σℓ/E の関係がありますから、（4）式は次のように書き換えることができます。

　（Aℓ/2E）σ² = Wh + (Wℓ/E)σ　　・・・（5）

二次方程式の解を求める公式により（5）式からσを求めれば、

　　　　・・・（6）

となります。

W/Aは、錘を静荷重として棒にかけたときの応力に等しく、これをσ0とします。
静荷重による伸びをλ₀とすれば、λ₀ =σ₀ℓ/E=Wℓ/AEです。
したがって、（6）式は次のように書き換えることができます。

　　　　・・・（7）

一般に、λ₀はhに比較して非常に小さい値ですから、錘の落下により生じる衝撃応力は、静荷重による応力に対して著しく大きくなることが（7）式からわかります。

h=0、つまり錘を棒下部のつば部にわずかに接触したような状態から急に放した場合でも、静荷重による応力の2倍ということになります
 

衝撃応力の計算例

一例として、質量M=10[kg]、棒の長さℓ=1[m]、棒の直径50[mm]として、h=0.5[m]から錘を落下させた場合の衝撃応力σを計算してみます。

　静荷重σ₀ =W/A =10×9.8/{(π/4)0.05²}=49911[Pa]

棒のヤング率を205[GPa]（一般的な鉄鋼材料）とすれば、

　λ₀ =σ0ℓ/E =49911×1/205×109=2.43×10^-7[m]

（7）式にσ₀とλ₀を代入して　σ=101.3[MPa] となります。

　101.3×10⁶/49911=2030

この例の場合、衝撃応力は静荷重による応力の2000倍を超える大きさということになります。

　　　　・・・（8）
 

最大曲げ応力・最大たわみ量の計算例

（7）（8）式の関係は、はりに衝撃荷重が加わったときに生じるたわみや曲げ応力を、静荷重の場合との比較で求めるときにも、全く同様に適用することができます。

図のように、中央部に集中荷重Wを受ける支持はりの断面二次モーメントをI、断面係数をZとすれば、材料力学の公式により、次のようになります。

　最大曲げ応力σ_b0=Wℓ/4Z　　・・・ (9)
　最大たわみ量δ₀=Wℓ³/48EI　　・・・ (10)

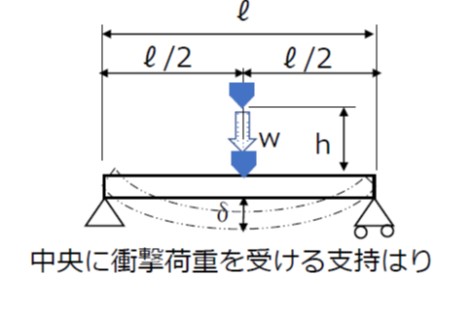
集中荷重に相当する質量（静荷重W=Mg）を、高さhの地点から垂直に落下させてはりの中央部に衝突させたときに生じる最大衝撃曲げ応力と、最大たわみは（7）（8）式のλをはりのたわみδに変えて

　　　　・・・（11）

　　　　・・・（12）

となります。

一例として、スパンℓ=1[m]、はりの部材をI型鋼200×100とします。

鉄鋼規格より、I=21700000mm⁴, Z=217000mm³
W=100[N]（質量10.2[kg]）とすれば、
（9）式より　σ_b0=0.115[MPa]　
（10）式より、δ₀=0.00047[mm]

これに対して、落下による衝撃の場合は、落下高さh=0.5[m]とすれば
（11）式より、σ_b=167.7[MPa]　
（12）式より、δ=0.686[mm]

この例の場合では、衝撃応力は静荷重による応力の1500倍に近い大きさとなります。
 

衝撃応力の計算は、実際にはかなり複雑で難しい

物体の落下や衝突など、部材に衝撃力が加わることが想定される場合は、上記の式により衝撃荷重による応力や伸び（たわみ）を計算して、部材の強度設計に反映させる必要があります。
ただし、この式は錘の持つ位置エネルギーが全て衝突した物体に内部エネルギーとして蓄えられるという仮定のもとに成り立ちます。

実際には、錘自身の変形、支持部の変形などもあり、また、衝撃応力は物体中を波動として伝わり、変動する複雑な現象です。あくまで衝撃応力を見積もるための目安と考えてください。
また、応力が弾性限度を超えると永久ひずみを生じて、ひずみエネルギーの多くが塑性変形に費やされるため、現象はさらに複雑となり、実験によって実際の応力を推定することも必要となります。

３．シャルピー衝撃試験

機械材料の衝撃荷重に対する抵抗力（粘り強さ、靭性）を知るために衝撃試験が行われます。
金属材料の靭性を判定するために通常よく実施されるのが、シャルピー衝撃試験です。
これはV形の切り込み（Vノッチ）を設けた試験片を、ハンマーを振り下ろして衝撃により破壊し、ハンマー振り下ろし位置に設定した時の持ち上げ角θαと、試験片破壊後に惰性で振り上がった振り上がり角θβから、試験片の破壊に要するエネルギーを求める試験です。
破壊後の振り上がり角が小さい（ハンマーが低い位置までしか振り上がらない）ほど、試験片が破壊するまでにより多くのエネルギーを吸収することができた、すなわち材料の靭性が高いことを示します。

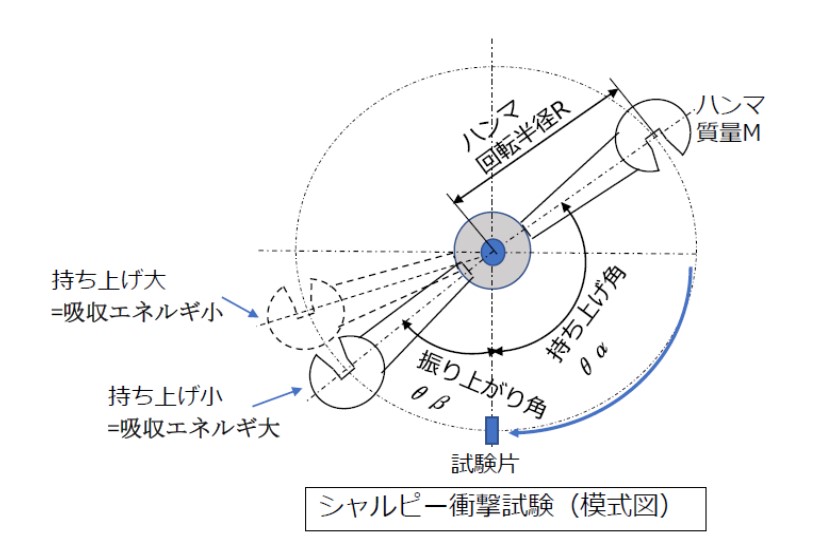
ハンマー質量をM[kg],腕の長さ（回転半径）をR[m]とすれば、吸収エネルギーEは次のようになります。
　E=Mg R (cosθβ‐cosθα)-L [J]　
　L：ハンマー回転の摩擦損失エネルギー

シャルピー衝撃値は、吸収エネルギーを試験片断面積で割った値で実用的には[J/cm²]が使用されています。
シャルピー衝撃値が高い材料は、切り欠きによる応力集中などがある場合でも、局部的に塑性変形することによって衝撃エネルギーを吸収することができて破壊しにくい、ということがいえます。

衝撃値の他に、試験時の温度と破面観察による評価を行うことも重要です。
同じ金属材料でも、温度が低いほど吸収エネルギーは低く、試験片の破面は脆性破面（銀白色で平ら）となります。高温になると吸収エネルギーが大きくなり、破面は延性破面（凹凸があって暗灰色）となります。
金属材料は一般的に低温になると靭性が低下するので注意が必要です。

［※低温脆性の解説は、別コラム「クリープ現象と低温脆性がこれでわかる！知っておきたい金属材料特性の基本」をご参照ください。）

（日本アイアール　特許調査部　S・Y）
 

Tweet

Pocket