【機械設計マスターへの道】次元解析のやり方とΠ定理（ポンプの模型試験の例で理解する）

Tweet

Pocket

当連載の前回のコラム［模型実験・模型試験に必要な「相似則」と「無次元数」の知識を整理］において、ポンプの模型試験を行うときは、幾何学的相似性と運動学的相似性を満足することで力学的相似性をも満足することができる、ということを書きました。

このことを理解するうえで重要な、次元解析とΠ定理の考え方について解説します。

１．次元解析

SI基本単位の中で、流体力学でよく扱うものは、質量kg、長さm、と時間s です。

単位の代りに、物理量Mass, Length, Timeの頭文字M,L,Tを[ ]で囲み、組立単位をその指数で表したものを「次元」といいます。
たとえば圧力の単位は、 Pa=N/m²=kg/(ms²) ですから、その次元は [ML^-1T^-2] となります。

次元解析は、ある物理量とそれに関係する諸因子の次元に関する同次性に基づいて物理量を表す方法です。
次元解析でよく用いるのが「指数法」と呼ばれる手法です。

[W]=[X]^a[Y]^b[Z]^c のような形で、対象とする物理量Wを、関連する諸因子X,Y,Zの、指数関数積の形で表し、物理量と諸因子の次元の整合から指数a,b,cを求め、対象とする物理量を表す式を求める方法です。次元解析を用いることで、様々な物理量を、数学的に簡潔明確に扱うことが可能になります。
 

２．バッキンガムのΠ定理

ある機械やシステムに関係のある物理量（物理現象）が m 個あって、各物理量を構成する基本単位がn個あるとするとき、機械やシステムの特性を支配する k=(m-n) 個の、独立した無次元積の方程式Πが存在します。これを「バッキンガムのΠ（パイ）定理」といいます。次元解析に用いる指数法を数学的に表現したものです。

m個の物理量のうち、基本単位数と同じn個は、指数関数の形でΠの式すべてに含むようにします。n個の物理量を「繰り返し変数」といいます。
残りのk=(m-n)個の物理量は、Πの式に一つずつ入れて、べき指数を通常は1とします。
物理量をt1,t2,・・・・・、tmとすれば、次のように表されます。

　Π₁= t₁^α1t₂^β1・・・t_n^ξ1t_（n+1）
　Π₂= t₁^α2t₂^β2・・・t_n^ξ2t_（n+2）
（省略）
　Π_k= t₁^αkt₂^βk・・・t_n^ξkt_m
・・・(1)

各式の左辺・右辺の次元を等しくおいたとき、左辺は無次元数であることから、[M⁰L⁰T⁰]となります。
これにより右辺各項のべき指数、α_1・・・k、 β_1・・・k、 ・・・、 ξ_1・・・k を求めることができ、k個の物理量t_（n+1）、t_（n+2）、・・・、t_m の各々と、繰り返し変数とした物理量 t₁、t₂、・・・、t_n との相関関係を把握することができます。
 

３．ターボ形ポンプにおける相似則

流体力学に用いる基本単位の個数nは、L，M，Tの3つです。

ターボ形ポンプ性能に関係する物理量として、流量Q、全圧P、軸動力W，回転速度N、流体密度ρ、羽根車直径D、の6つが考えられます。
したがって、m=6,n=3,k=6-3=3 ということになります。

流量、全圧、軸動力という特性は、回転速度、密度、羽根車直径のすべてに依存するので、この3つを繰り返し変数とします。
すると(1)式を、次の(2)式のようなk=3個の無次元積として表すことができます。

　Π₁=D^α1N^β1ρ^γ1Q
　Π₂=D^α2N^β2ρ^γ2P
　Π₃=D^α3N^β3ρ^γ3W
・・・(2)

6個の物理量の次元は、Q[L³T^-1]、P[ML^-1T^-2]、W[ML²T^-3]、N[T^-1]、ρ[ML^-3]、D[L] となります。
したがって、（2）式右辺の各物理量をそれぞれの次元で表し、左辺が無次元数となるべき指数α₁,α₂，・・・・・・γ₃を求めることによって、次のようになります。

　Π₁=Q/(D³N)、Π₂=P/(ρD²N²）、Π₃=W/(ρD⁵n³）　　・・・(3)

（1）幾何学的相似性

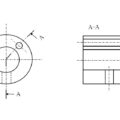
模型試験を行うとき、実機と模型の羽根車直径比と同一の縮尺に忠実に、模型の各寸法（羽根車入口径、入口出口流路幅、ケーシング各部寸法、主軸径、など）を決定すれば幾何学的相似性が得られます。

実機にp、模型にmの添え字をつけて表すことにします。実機と模型の羽根車直径比Dp/Dmをモデル比といいます。(3)式より、流量はモデル比の3乗に、全揚程（全圧P/ρg）はモデル比の2乗に、軸動力はモデル比の5乗に、それぞれ比例することがわかります。また流量は回転速度比N_p/N_mに、全揚程はN_p/N_mの2乗に、軸動力はN_p/N_mの3乗に、それぞれ比例することがわかります。
 

（2）運動学的相似性

運動学的相似性についても考えてみます。
 
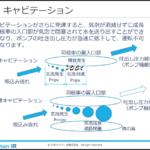
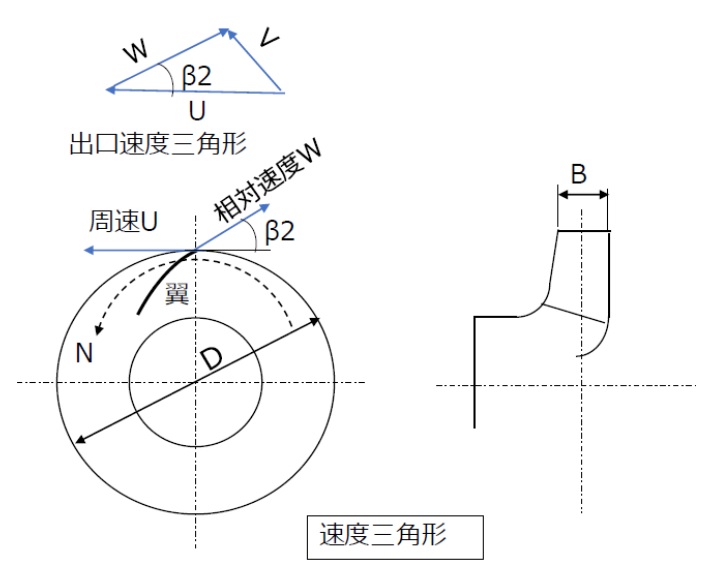
ターボ形ポンプの羽根車の翼は、図のように回転方向に対して後向きに湾曲した形状です。羽根車直径先端部で翼は回転方向に、周速度U=πDN/60[m/s] の速度成分を有しています。（D[m],N[min^-1]）

　Up/Um=(πDpNp/60)/ (πDmNm/60)= (Dp/Dm)(Np/Nm) 　　・・・(4)

一方、羽根車を通過した水は、翼の出口角度β方向に相対速度W[m/s]で流出します。
静止座標系から見たとき水は、周速Uと相対速度Wをベクトル合成した方向へ絶対速度V[m/s]で流れます。U,W,Vからなる三角形を「速度三角形」といいます。

絶対速度は流量を羽根車の出口面積で割った値ですから、羽根車出口の流路幅をBとおけばV=Q/(πDB)となります。幾何学的相似性よりBp/Bm=Dp/Dmです。

　Vp/Vm=( Qp/Qm)/{(πDpBp)/(πDmBm}=(Dp/Dm)³Np/Nm/(Dp/Dm)²=(Dp/Dm)(Np/Nm) 　　・・・(5)

(4),(5)式より、速度三角形もモデル比と回転速度比に比例するので、羽根車の翼角度βや曲面形状を含めて実機に対する模型の幾何学的相似性を確保することで、運動学的相似性も保たれることがわかります。
図は、翼出口の速度三角形を示していますがが、入り口についても同様な相似性が要求されます。

全揚程および軸動力についても同様の検証をすることが可能ですが、省略します。

なお、ある程度以上のレイノルズ数(Re)では、ポンプ特性はReを変えてもほとんど変化しません。完全な乱流で粘性による力に対して慣性力の方が支配的になるためです。

また、ポンプ特性は、流路壁面の表面粗さや、摺動すき間からの漏れにより変化します。一般的に小型ポンプの方が表面粗さや漏れ量の影響が大きく、模型試験で得られた性能を実機換算するときモデル比に応じて特性の補正を行います。
寸法比による特性変化を「寸法効果」といいます。
 

４．比速度の無次元化

ポンプに関する別の連載コラム、「ターボポンプの比速度と吸込比速度」で、比速度Nsには単位があるということを説明しています。
式（3）のΠ1,Π2 から、新たな無次元数Π₄ を得ることができます。

　Π₄=Π₁^1/2/Π₂^3/4 =(Q/D³N) ^1/2/(P/ρD²N²) ^3/4=(Q/D³N) ^1/2/(ρgH/ρD²N²) ^3/4
=N√Q/(gH) ^3/4　　・・・(6)

(6)式Π₄は、比速度Nsの分母を、重力加速度gの3/4乗で割った値です。

国際規格ISOでは、回転速度N[min-1]に替わり、回転角速度ω[rad/s]を用いた無次元数χ（カイ）を用いています。χを「形式数」(Type Number)といいます。
（6）式のgHを⊿Eとおけば、χ=（2πN/60）｛√Q/（⊿E）^3/4｝となります。

流量、全揚程の単位には関係ない普遍的な無次元数として、羽根車の相似性を表す指標として用いることができます。
 

（日本アイアール　特許調査部　S・Y）
 

Tweet

Pocket