模型試験に必要な相似則と無次元数を徹底解説!

大型の船舶、あるいは大型のポンプ、水車などの流体機械で、実機を用いて工場性能試験を行うことが現実的ではない場合、小型の模型を作って性能試験を行い、実機性能に換算して評価することが行われます。
今回のコラムでは、模型試験の結果から実機性能を保証するための、模型と実物の間の相似則と、相似性を表すため無次元数について見ていきたいと思います。
目次
1.3つの相似条件
相似というと、プラモデルで何分の1スケール、というように形状が同じで大きさが異なるもの、というように考えられますが、厳密には次の3つの相似条件があります。
模式的に示すと下図のようになります。
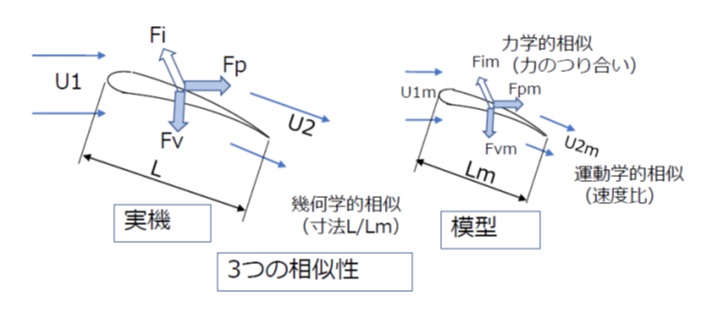
(1)幾何学的相似
「幾何学的相似」とは、実機と模型の間の寸法比をすべて等しくすることを指します。
寸法比をモデル比といいます。
模型の各部位の縦横高さの3次元寸法をモデル比に忠実に製作します。
(2)運動学的相似
「運動学的相似」は、実機と模型の間で対応する空間的・時間的な点、すなわち流線上の任意の位置における速度比が等しくなることをいいます。
ポンプや水車の羽根の丸みや曲がり具合など、流れに相対する形状や角度などの諸元も、実機と模型の間に正確な相似性が確立している必要があります。
(3)力学的相似
「力学的相似」は、実機と模型の間で対応する任意の位置で流体要素に作用する力の比が等しくなることをいいます。
《流体要素に影響する外力の種類》
流体要素に対して影響を与える外力として、次の5種類があります。
① 圧力による力Fp
圧力p、圧力が作用する断面積をAとすれば、
Fp=pA
となります。
② 粘性力Fv
ニュートンの粘性の法則による力で、粘性係数と速度勾配に比例します。
流体の粘度をμ、速度u, 流れに平行な壁面からの距離をyとすれば、
Fv=μ(du/dy)A
となります。
③ 重力Fg
流体に限らずよく知られているように、質量mと重力加速度gの積です。
Fg=mg
④ 弾性力Fe
流体の圧縮により発生する力です。圧縮に伴う圧力変化量と面積の積であって、体積弾性係数と圧縮による体積減少比に比例します。
流体の体積弾性係数をK,体積V,体積変化量⊿Vとすれば、
Fe=⊿pA={K(⊿V/V)}A
となります。
⑤ 表面張力による力Fs
流体の表面張力σ[N/m]に代表長さLをかけた値です。
Fs=σL
2.力学的相似性を確認するために用いる無次元数
力学的相似性を議論するとき、上述の5種類の外力がすべて相似となるようにすることは困難です。
そこで模型試験を行う対象となる機械における流れに最も影響を及ぼす外力に着目して、その外力が慣性力Fi [-(質量x加速度)] と釣り合っている状態を考えます。
慣性力は、物体に作用する力の平衡状態を考えるときの仮想的な力で、質量x加速度mαにマイナス符号をつけたものです。(ダランベールの原理)
このとき、実機と模型との間で、外力とマイナスを取った慣性力との比が等しければ、力学的相似条件を満足しているということができます。
この比は、力を力で割った値ですから無次元数になります。
船や飛行機、あるいは流体機械を設計したり模型試験を行ったりするとき、力学的相似性について確認するために用いる無次元数には次のようなものがあります。
ここで、長さと速度に関する物理量はすべて、代表長さL、代表速度U、のべき乗の形で表すことにします。(例えば、面積AはL2の形で表すことにします。)
(1)レイノルズ数Re
自由表面が存在せず(表面張力の影響を受けない)、重力や浮力の影響を受けず、圧縮性の影響を無視できる(弾性力の影響を受けない)という条件下では、粘性力Fvと慣性力の比である「レイノルズ数」が重要な無次元数となります。(レイノルズ数の解説は「管路における圧力損失の考え方と計算」の回もご参照ください。)
Re=慣性力/粘性力=mα/μ(du/dy)A=ρU2L2/(μUL)=ρUL/μ=UL/ν
ここでρは流体の密度、μは粘度、νは動粘度μ/ρ です。
レイノルズ数は、水中を進む潜水艦や、空気中を低速で進む飛行船、ポンプ・水車などの非圧縮性流体機械における運動解析や模型実験を行う際の指標として利用されます。
管路内の流れであれば、円管であれば直径、円管以外であれば水力直径が代表長さL、管内平均流速が代表速度Uとなりますが、流れの中に置かれる機械・物体の場合は、対象によってL,Uは異なってきます。
ポンプの場合は、代表長さLとして羽根車の直径、代表速度Uとして羽根車の周速度を用いることが一般的です。ポンプの模型試験をおこなうとき、レイノルズ数を実機と模型で一致させることは現実的でないことが多く、一方ポンプにおけるレイノルズ数は十分に大きくレイノルズ数が変化してもポンプ特性はほとんど変化しません。
このため、レイノルズ数をある値以上としたうえで、模型試験における運動学的相似性の確保をもって力学的相似性も満足するようにします。
(2)フルード数Fr
船舶は、自由表面である水面に浮かびながら波を立てて進みますので、粘性よりも重力の方が支配的と考えます。
この場合、慣性力と重力Fgの比の平方根をとった無次元数フルード数Frが重要となります。
Fr =√(mα/mg)=√(ρU2L2/ρL3g) =U/√gL
船の場合は、一般的に代表長さLとして船の全長を用います。
フルード数は、船舶の他にも、橋脚、水門、ダム、などの設計にも利用されます。
水槽における船の模型実験を行う際は、フルード数が実物条件と一致するように模型船の速度を設定します。
また、船が進むときに受ける造波抵抗係数は、フルード数の関数として表されます。
(3)マッハ数M
圧縮性が支配的な因子となる場合は、圧縮に要する力である弾性力を考えます。
慣性力と弾性力Feの比の平方根をとった無次元数をマッハ数Mといいます。
M=√(mα/(⊿pA)) =√mα/[{K(⊿V/V)}A]=√(ρU2L2/KL2) =U/√((K/ρ)=U/a
流体の中を圧力変化が波として伝播する速度を「音速」といい、音速 a=√((K/ρ) です。
すなわち、代表速度と音速の比がマッハ数です。
旅客機などでよく超音速といいますが、M>1.2の場合が「超音速」で、ロケットなどでM>5になると「極超音速」と呼びます。M<0.3になると非圧縮性として扱うことが可能です。
常温常圧における音速は340m/sですから、M=0.3 は 340×0.3×3600/60=367km/h
新幹線は、非圧縮性として扱うことのできる上限の領域ということができます。
リニアモーターカーは時速500km/hに達するので、M=0.4となって圧縮性の影響を考慮する必要があることになります。
なお、風洞を使って飛行機の模型実験を行うときなどは、マッハ数が実機と一致するように風洞の速度を設定します。
(4)オイラー数E
圧力の影響が大きいとき、慣性力と圧力による力Fpの比が重要となります。
E=mα/Fp= mα/pA=ρU2L2/pL2 =ρU2/p
Eをオイラー数といいます。
流れの中に置かれた物体に作用する抵抗や、管内流れの抵抗損失を考えるときに重要な指標となります。
また1/2ρU2 は動圧とよばれる運動エネルギであり、オイラー数は動圧と静圧の比に関する無次元数ということもできます。
(5)ウェーバ数We
慣性力と表面張力による力Fsの比の平方根をとった無次元数をウェーバ数Weといいます。
We= √(mα/(σL)= √(ρU2L2/σL)=U√(ρL/σ)
表面張力の大きい液滴の問題を考えるときなどに重要となる指標です。
このように流体機械や流体中を進む物体の、性能・特性や関連する様々な事象を検討する際に、その流れ場の中で支配的となる外力に応じた無次元数を適切に使い分けることが重要となります。
次回の連載では、力学的相似性を理解するうえで必要な次元解析とΠ定理の考え方を解説します。
(日本アイアール 特許調査部 S・Y)