【機械設計マスターへの道】骨組構造「トラス」と「ラーメン」を理解する（構造力学の基礎知識）

Tweet

Pocket

今回は、構造力学に出てくるトラスとラーメンについて考えてみます。

１．骨組み構造と支点

複数本の直線状の部材の端部を連結して、荷重を安全に支え得るようにしたものを「骨組構造」といいます。
部材端部の連結点「節点」といい、部材が自由に回転できる節点を「滑節」、部材同士のなす角度が一定となるよう固定したものを「剛節」といいます。

「はり」と同様に、骨組構造の支点には、回転自由で移動を許さない回転支点、回転のほかに一方向にのみ移動が許される移動支点、回転・移動ともに許さない固定支点、の3つがあります。節点と支点の図示記号を図1に示します。

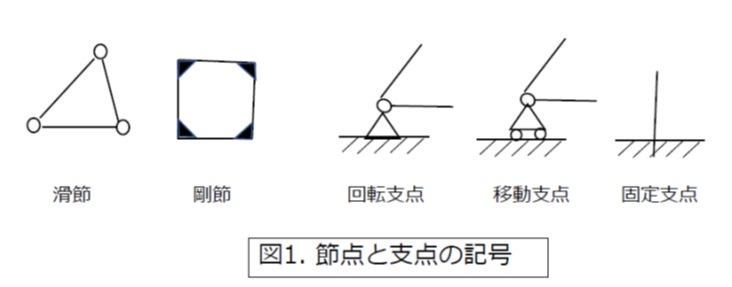
回転支点における反力は水平・垂直の二分力を持ち、移動支点では移動方向に対して垂直な分力のみを持ちます。固定支点には、水平・垂直の二分力のほかに曲げモーメントが作用します。
 

２．「トラス」とは？

全ての節点が滑節で、支点が回転支点または移動支点である骨組構造を「トラス」といいます。
トラスの節点はボルトやピンなどで結合されています。

トラスの支点は回転支点または移動支点であって相互運動が可能なように結合しているので、曲げモーメントが作用しません。荷重に対して、部材には引張または圧縮の力（軸力）のみが作用します。
 

（1）トラス構造

トラス構造は、図2のような三角形に組んだ部材の組合せからなっています。

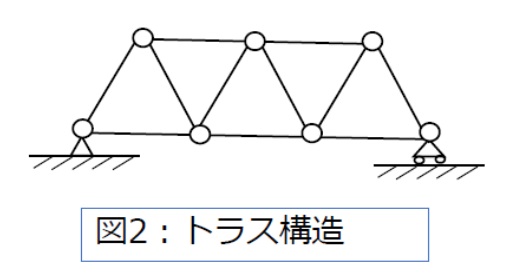
トラスの部材に生じる内力と支点反力が、荷重に対するつりあい条件のみから直接決定できるものを「静定トラス」、部材の弾性変形をも考慮しなければ決定できないものを「不静定トラス」といいます。

静定トラスの解放には「節点法」と「切断法」とがあります。
 

① 節点法

「節点法」は、各節点における反力を求め、水平・垂直方向のつり合い条件から、部材に作用する軸力（引張・圧縮）を求める方法です。
適用条件として、節点につながる軸力が未知である部材の数を2以下とする、という点に注意が必要です。
したがって、軸力の計算は先ず一番端の節点を挟む2本の部材から始め、順次隣の節点を挟む軸力未知の2本の部材の軸力計算、というように中央部分へ向けて展開していくことになります。
 

② 切断法

「切断法」は、軸力を求めようとする部材を含む3本の部材をトラスから切り出して、分割した部分に対する外力の3つのつり合い条件から軸力を計算する方法です。
トラス全部材の軸力を計算しなくても、軸力を知りたい部材の軸力だけを求めることができます。
中央部付近の部材の軸力をすばやく求めたいときなどに便利です。

3つのつり合い条件として、水平分力、垂直分力、と1節点まわりの力のモーメントのつり合いから部材軸力を求める「カルマン法」と、同一直線上にない3節点まわりの力のモーメントのつり合いから部材軸力を求める「リッター法」とがあります。

（2）部材の応力にどの程度の違いが生じるか？

次に支持はりの場合と、トラス構造にした場合とで、部材の応力にどの程度の違いが生じるか、簡単な例で考えてみたいと思います。

図4左は、中央に集中荷重Pが作用するスパンℓの支持はり、右は正三角形からなる簡単なトラスで頂点の節点に荷重Pが作用しています。部材は高さｈ 幅ｂ の長方形の一葉断面であるとします。

右のトラス構造部材の軸力を節点法で求めてみます。
正三角形で左右対称であることから、支点反力 Ra=Rb=P/2、各部材に生じる軸力をF1，F2，F3とします。
各節点で垂直分力と水平分力の和は、ともにゼロとなります。

幾何学的関係より、
　節点Ａにおける水平分力つり合いは、F1+F2cos45°=0　　・・・(1)　
　節点Ａにおける垂直分力つり合いは、Ra+F2sin45°=0　　・・・(2)

(2)式より、F2=-Ra/sin45°=-P/(2 sin45°) （圧縮）
(1)式より、F1=-(-P/(2 sin45°) cos45°=P/2　（引張）

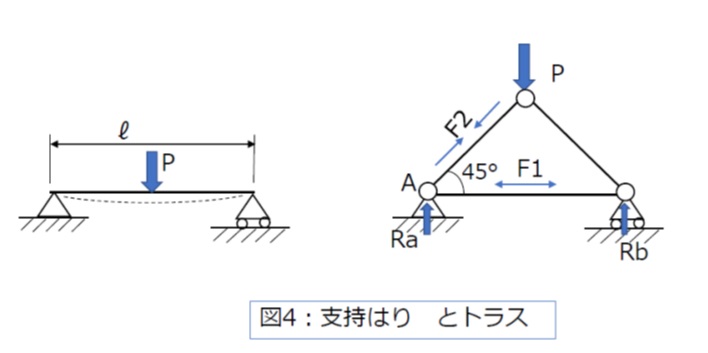
P=1000[N], h=13[mm],b=6[mm]であるとすれば、
水平部材に生じる引張応力σは F1(=P/2) を部材断面積で割った値ですから、
　σ=1000/(2x6x13)=6.4[N/mm²](MPa)

支持はりの場合、最大曲げモーメントは、はりの中央部で生じ、
　Mmax=Pℓ/4
スパンℓ=100[mm]であるとすれば、
　Mmax=1000×100/4=25000[N・mm]
部材の断面係数
　Z=bh2/6=6x13x13/6=169[mm³]
部材に生じる最大曲げ応力は、
　σbmax=Mmax/Z=25000/169=148[N/mm²](MPa)
となります。

はりをトラス構造とすることで応力を曲げ応力から軸応力（引張応力または圧縮応力）に変換し、同一荷重に対して生じる応力値を極めて小さくすることができます。
 

３．「ラーメン」とは？

全ての節点が回転できず、部材同士のなす角度が一定になるよう固定した剛節からなる骨組構造を「ラーメン」といいます。

節点が自由に回転することができないため、部材には軸力の他に、曲げモーメントが作用します。
ラーメンは一般的に不静定構造となるので力のつり合い条件だけから解くことはできません。
通常は、変形は微小でかつせん断による変形は無視できるものとして、単に部材の曲げによる変形のみを考えて不静定はりとして解きます。

トラスが三角形の骨組構造であるのに対して、ラーメンは四角形の骨組構造です。
荷重に対する変形を軽減するため、図5のように四隅の剛節に補強材を配して強度を高めます。

ラーメンは荷重を曲げモーメントで受けるため、強度的な観点からは軸力で受けるトラスの方が有利と考えられます。このため大型の橋梁、タワー、あるいは二輪車のフレームなどにトラスが用いられます。
一方、トラスは三角形の骨組で斜めに部材が配されるため、横切って人や物が出入りするのには不都合な面があります。

その点ラーメンは四角形で開口を大きく取ることができるので、オフィスビルやマンションなどの建築物、あるいは内部に設置した機械の操作や保守が必要な機械装置架台などには、ラーメン構造が多く採用されます。
 

（日本アイアール　特許調査部　S・Y）
 

Tweet

Pocket