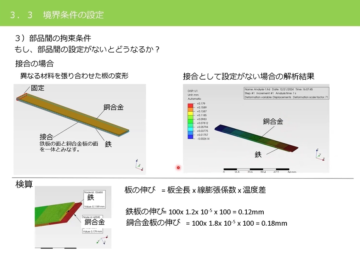
【機械設計マスターへの道】三次元応力と破壊学説
実際の機械や構造体では、作用する荷重と発生する応力が一方向という単純な場合は少なく、多くの場合は、荷重に応じて発生する垂直応力とせん断応力とが様々な方向へ作用する三次元応力の組合せ状態になります。
1.主応力、主せん断応力
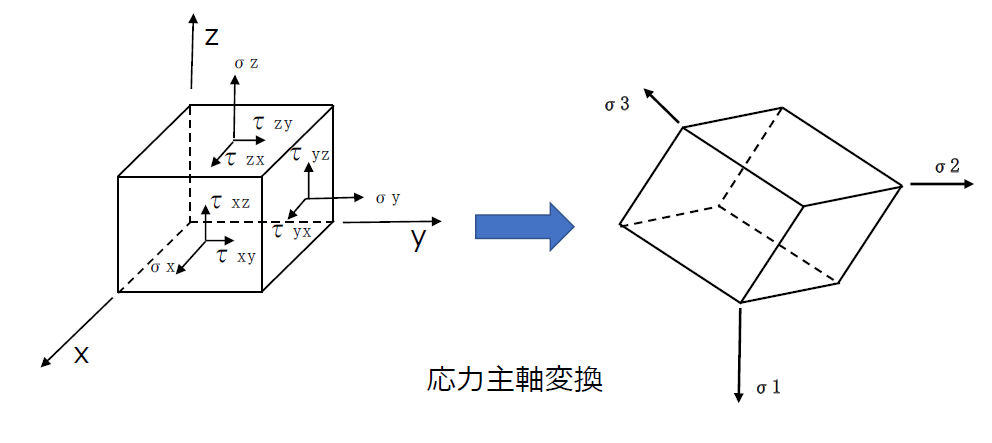
立体形状の物体に生じる三次元応力を考えるとき、応力成分を定義する直交する3つの軸を変換して選ぶことにより、せん断応力成分がすべて0で、垂直応力成分のみとすることができます。
このときの3軸を応力の主軸と呼び、3軸方向の垂直応力の値を「主応力」といいます。主応力の作用面は「主応力面」と呼びます。
3軸方向の垂直応力をσ1,σ2,σ3とするとき、そのうちの最大値を最大主応力σmaxと呼びます。
各軸方向の主応力に対するひずみを「主ひずみ」といい、軸ごとにε1、ε2、ε3とするとき、次の関係があります。
ε1=(σ1-ν(σ2+σ3))/E
ε2=(σ2-ν(σ3+σ1))/E
ε3=(σ3-ν(σ1+σ2))/E
E:ヤング率、 ν:ポアソン比
(※ヤング率とポアソン比については、連載コラム「荷重、応力、ひずみ」の回をご参照ください)
応力の主軸を選ぶことで、せん断応力成分は0となりますが、物体内部に発生するせん断応力そのものが0になるという意味ではありません。
三次元応力状態では、せん断応力にも3つの極値が存在し、これを「主せん断応力」といいます。
せん断応力が最大、最小となる面を「主せん断応力面」と呼び、主応力面に対して45°の傾きをなします。
各方向の主せん断応力をτ1、τ2、τ3とするとき、3つの主応力から次の式によりその値を求めることができます。
τ1=±(σ2-σ3))/2
τ2=±(σ3-σ1))/2
τ3=±(σ1-σ2))/2
このうちの最大値を、最大せん断応力τmaxとよびます。
2.ひずみエネルギー
座標軸を、上記1.で説明した応力の主軸と一致させたとき、3次元応力状態で材料が受ける各主応力によって材料に蓄えられるひずみエネルギーU0を次式で求めることができます。
U0=(1-2ν)(σ1+σ2+σ3)2/6E+(τ12+τ22+τ32)/3G
G:横弾性係数
(※横弾性係数については、「荷重、応力、ひずみ」の回をご参照ください)
この式の第1項は主応力による体積変化に費やされるひずみエネルギを、第2項は主せん断応力による形状変化に費やされるひずみエネルギを表し、第2項のことを、せん断ひずみエネルギUdとよびます。
3.破壊学説
機械の部材が、応力を受けて破壊に至るのは何が主要因なのか、について様々な学説があります。
(1)最大応力説
材料内部のある点に生じる3つの主応力σ1、σ2、σ3のうち、いずれかが降伏点に達すると破損が発生し、いずれかが引張強さに達した時に破壊するという説です。
この説は、延性材料に対しては正確にはあてはまらないが、脆性材料に対しては実験結果と良い一致を示します。
(2)最大せん断応力説
最大せん断応力が、最大せん断降伏点(または0.2%耐力)に達すると塑性変形するとする説です。
応力の主軸に対して、最大せん断応力は軸と45°をなす面に生じることから、降伏応力σysと、降伏せん断応力τyの間には次式の関係があります。
σys=2τy
上記1.において説明した、主せん断応力と主応力の関係から展開して考えると、降伏条件は次式となり、これをトレスカ(Tresca)の降伏条件式といいます。
σys=max(|σ1-σ2|,|σ2-σ3|,|σ3-σ1|)
部材内部のある1点に生じる主応力がσ1>σ2>σ3 の関係にあるとき、降伏条件はσ1-σ3 となって、中間の大きさの主応力σ2とは無関係になります。
この説は、延性材料に対して実験結果とよい一致を示します。
(3)せん断ひずみエネルギー説
ミゼス(Von Mises)の降伏条件式ともよばれ、材料の単位体積当たりに蓄えられるせん断ひずみエネルギーが、材料に固有なある値に達した時、塑性変形が生じるとする説です。
上記2.において掲載した式の第2項であるひずみエネルギUdと主応力の間には次の関係があります。
(τ12+τ22+τ32)/3G=(1+ν)((σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2)/6E
これより降伏応力σysは次式で表されます。
σys2=((σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2)/2
延性材料に対しては、最大せん断応力説よりも実験結果とよく一致することが多いといわれています。
なお、上式で計算される応力はミーゼス応力と呼ばれ、主応力と異なり方向性をもたない正のスカラ量です。
材料の単軸降伏応力と等価に比較することができるので、延性材料の強度評価に良く用いられます。
ただし、スカラ量なので応力の方向であるとか、引張なのか圧縮なのかについては区別がつきませんので、主応力についても確認する必要があります。
機械設計において、強度部材の応力を有限要素法解析により求めることが行われます。
解析で得られた応力が、主応力なのかミーゼス応力なのかをよく確認して設計に反映するようにしましょう。
次回の連載コラムでは、柱が圧縮力を受ける際に、応力自体は低くても不安定な変形が生じてしまう「座屈」という現象について説明いたします。
(日本アイアール株式会社 特許調査部 S・Y)
《併せて読みたい関連コラム》
- 「主応力とモールの応力円の求め方」はこちら