《実験計画法と統計》推定と仮説検定の考え方
はじめに：実験計画法と統計
あなたは、果物屋さんでおいしい桃を見分ける方法はないかと考えています。
「どれを選べば甘いのか」がわかるでしょうか？
今日はたくさん桃を買って甘さに何が関係しているのかを調べ、次回からは甘い桃を選べるようにしようと考えました。
実際にどのように調べていけば、効率的に甘い桃の基準を調べることができるでしょうか？
どんな要因が甘さに関係するかを考えます。
「サイズ」「色」「香り」「かたさ」・・・
お店で商品にさわらないように見た目で判断できる、「サイズ」と「色」に着目しました。
甘さは糖度を調べる糖度計を用いて測定することにしました。
【表1 桃の色とサイズ毎の糖度のデータ】
果物屋さんから、
サイズが大きくて、色が濃い、薄い、
サイズが中くらいで、色が濃い、薄い、
サイズが小さくて、色が濃い、薄い、
をそれぞれ２個、計１２個買ってきて、桃の糖度を調べて、平均値をだしました。
表1は測定した糖度の値を、サイズと色で整理した結果です。
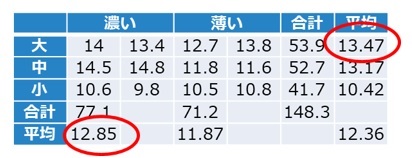
サイズでは「大」、色では「濃い」の平均値が最大値となりました。
でもこれは本当に意味のある差でしょうか？
一つ一つの桃の糖度がこれだけ違っているのに、今回買ってきた桃と果物屋さんに並んでいる桃が同じ様なものだと言えるでしょうか？
この表から何がわかるのか、いっしょに考えていきましょう！
当連載コラム「これならわかる実験計画法入門」では、前回まで6回にわたり実験計画法の概要と最重要知識を解説してきました。今回からは「統計編」と位置付けて、おいしい桃の見分け方をみつけるための実験を例に、実験計画の立て方と、実験結果の分析方法を説明します。
実験計画法では以下の2つのステップを行います。
- 効率の良い実験方法の計画を行う
- 得られた実験データを適切に分析する
実験計画法を使うとお店の桃について、
「どの要因が桃の甘さに影響があるか」
「要因の最適な条件は何か」
さらには、「これらのことがどの位の確かさで言えるのか」を、
統計学を用いて客観的に判断することができます。
１．統計学の基本用語
ここからしばらくは、桃の甘さを調べる実験を例に、統計学で使われる用語について説明していきます。
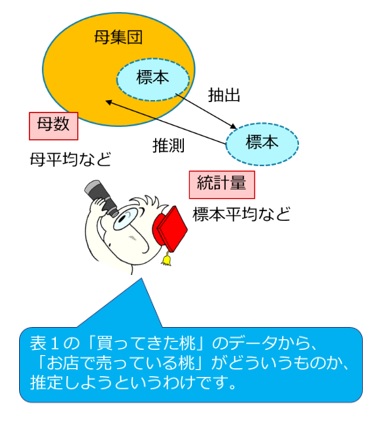
統計学ではお店で売っているすべての桃は「母集団」といい実験や調査の対象となる全ての集合を指し、買ってきた桃のように母集団から抽出した部分集合を「標本」といいます。
すべての桃を調べることは難しいので、母集団から一部をランダムに取り出して（抽出）調べ、標本から得られる特性を表す数値（統計量）から母集団の特性を表す数値（母数）を推定することを、推測統計学といいます。標本から母集団の様子を探るときに、「推定」と「仮説検定」という手法を用います。
２．推定の考え方と注意点（点推定と区間推定）
「推定」は、標本のデータから母集団の特性値を推し量ることを言います。
母集団の特性値に最も近いであろう値を推定する「点推定」と、推定誤差を考慮した「区間推定」があります。区間推定では、特性値が含まれるであろう推定値の幅（信頼区間）を求めます。
例えば、お店にある桃の糖度の平均値を推測する場合、点推定では、下のような表現をします。
お店にある桃の糖度の平均値の点推定値は12.36である。
同じように、お店にある桃の糖度の平均値を推測する場合、区間推定では、下のような表現をします。
お店にある桃の糖度の平均値は、信頼率95％で、区間12.00～12.72に入る。
いずれの場合も推定しているのは、糖度の平均値であることに注意して下さい。桃の一つ一つがどのような糖度になっているかについては何の情報もありません。
ことに区間推定の場合、「一つ一つの桃の糖度を測ってみると、95%がこの範囲に入っている」という意味ではありません。
また、正確に言えば、「お店にある桃の糖度の平均値」は確定しているので、お店の桃の糖度の平均値が確率変数であるかのような、上記の区間推定の表現は適切ではない＊という議論もありますが、感覚的には、「お店にある桃の糖度の平均値」がこの範囲にある可能性が高いと判断して良いと思います。
そこで、二つの推定値のイメージを図で示すと下のようになります。
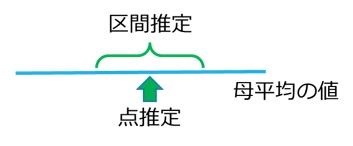
＊：「母集団から標本をとりだし、その標本から母平均の95%信頼区間を求める」ことを100回繰り返したとき、ほぼ95回はその区間内に母平均が入る」というややこしい表現になります。
４．仮説検定の考え方と注意点
「仮説検定」は、母集団の特性についての予想が正しいかどうかを、標本データから確率的な尺度を用いて判断する方法です。
例えば、「お店の桃のサイズと糖度は相関している」という仮説が正しいかどうか判断するために行います。
仮説検定では、本当は言いたいこと、
「お店の桃のサイズと糖度は相関している」（対立仮説）
を証明するためにいったん、
「お店の桃のサイズと糖度は相関してない」（帰無仮説）
と仮定します。
帰無仮説が正しいと仮定して、得られているデータが起こる確率を計算してみます。
その確率が十分小さく、めったに起こらないと言えるのであれば、帰無仮説は正しくないと判断します。このことを、「帰無仮説を棄却する」と言います。
有意水準と帰無仮説
仮説検定の手順を、極端な例を使って説明します。
「サイズと糖度は相関していない」という仮説をたてます。
12個の桃についてサイズと糖度のデータを取ってみたら下のような結果でした。
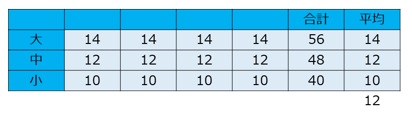
この結果から、次のような理屈が成り立ちます。
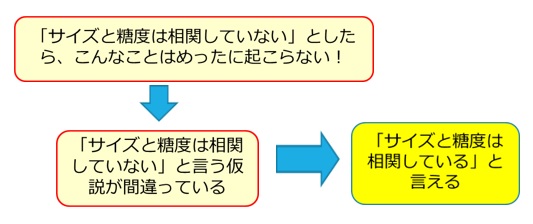
「サイズと糖度が相関しているからこのようなデータが得られるのだ」と言うのではなく、「サイズと糖度が相関していないとすればこのようなデータは得られないはずだ。ということはサイズと糖度が相関しているということだ」という理屈です。
上では、直感的に「めったに起こらない」としましたが、仮説検定では「めったに起こらない」かどうかを、得られているデータが起こる確率から判断します。つまり、その確率が十分小さく、めったに起こらないと言えるのであれば、帰無仮説は正しくないと判断します。
確率が十分小さいと言えるかどうかの判断基準（例えば5%以下、1%以下など）を「有意水準」と言います。
これを図で示すと、下のようになります。
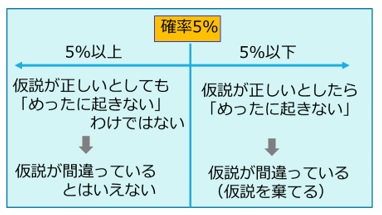
ここで注意しなければならないのは、確率が有意水準以下だったとしても、めったに起こらないことが起こったというだけなので、帰無仮説が完全に間違いとは言えないということです。
有意水準5％で帰無仮説を棄却するということは、危険率5％で正しい仮説を否定するということになります。
なお、このような手順で、帰無仮説が間違っていると判断できなかった場合でも、対立仮説が正しくないとは言えないことには注意して下さい。単に証拠が不十分であったというだけで、どちらが正しいかの結論は出ていない状態です。
さて、先ほど例に示した表（買ってきた桃の糖度を調べた結果）をもう一度みてみましょう。
【表1（再掲） 桃の色とサイズ毎の糖度のデータ】
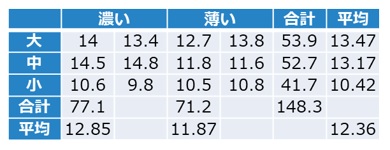
この表からは、平均的に言って、大きい桃の方が糖度が高いような傾向は見えますが、「サイズと糖度は相関していない」と仮定したらめったに起こりえないと言えるほどの差でしょうか？
実は、この疑問に対して合理的な答えをくれるのが、後で説明する分散分析法ですが、その前に、分散分析法を理解するのに必要になる「ばらつき」の概念について知っておく必要があります。
（日本アイアール株式会社 H・N)
