実験データの分析から結果検証までのポイント《分散分析、最適水準の検討など》
当連載コラムの前々回「《実験の手順》要因配置実験と直交配列表実験のポイント」と、前回の「《実験順序》乱塊法と分割法をわかりやすく解説」では、実験の計画から実施までの段階を説明しました。
今回は「実験で得られたデータをどう分析し、さらにその結果をどのように検証するか」を説明します。
１．「データの分析」から「結果の検証」の手順
データの分析から結果の検証までは、以下の手順で行います。
（1）データの分析
- 実験データから分析に用いる数値を取りまとめ、グラフで視覚化し、要因効果を検証します。
- 要因効果があるか分散分析で検討し、要因効果のあった主効果や交互作用を特定します。
- 特性を最も高める最適水準を求めます。
- 特性値の母平均の推定など行います。
（2）結果の検証
- 求めた最適水準が適切かどうか検証し、必要があれば確認実験を行います。
- 明らかになった要因効果をもとに、新たに水準値設定など行い、次に実施する実験計画をたてます。
２．データの視覚化
当連載コラムの第１回「なぜ実験計画法が必要なのか？」で取り上げた、鰹節のだしを取る際にうまみと雑味のバランスが良い条件を見つける実験を例として、データの視覚化について考えます。
実験は、繰り返しのある二元配置実験で、図1のようなデータが得られました。
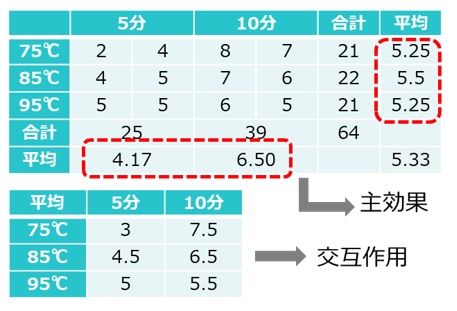
【図1 鰹節のだしのうまみと雑味のバランスが良い条件を見つける実験】
要因効果を見るために、味の評価を行ったデータの各因子の水準ごとの平均値、因子の水準組み合わせの平均値をグラフ化したのが図2です。
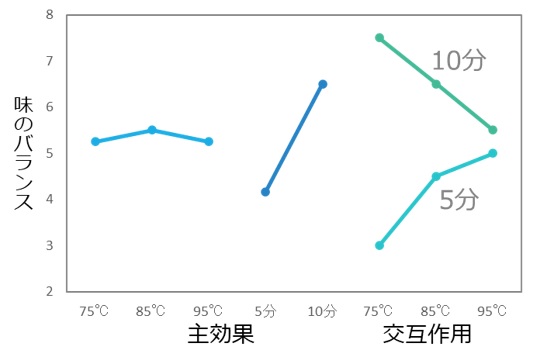
【図2 鰹節のだしの味の評価の平均値グラフ】
グラフ化した結果、時間の主効果、温度と時間の交互作用がありそうに見えます。このようにグラフ化すると、視覚的に要因効果を検証できます。
しかし本当に有意差があるかは、分散分析で見ることになります。
３．分散分析による検証
各々の手法を用いて、実験を実施して取得したデータに統計的に意味のある差があるかを検証します。ここでは分散分析を使って説明します。
「分散分析」は、分散（数値データのばらつき具合を表すための指標）を使って平均値を分析する手法です。
因子の水準の変化により特性値への効果があったかを評価したい場合、図3のように2種類のばらつきを見る必要があります。
「誤差によるばらつき」と、水準変化に伴い生じたデータの平均値の変化（ばらつき）である「要因の効果によるばらつき」です。
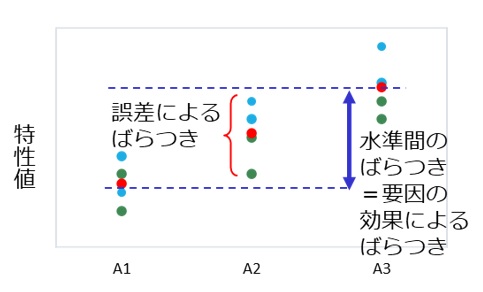
【図3 分散分析（誤差によるばらつき／要因の効果によるばらつき）】
要因の効果があるとすれば、要因の効果によるばらつきが、誤差によるばらつきよりも大きくなるはずです。
図3の場合、A1、A2、A3の水準の違いによるばらつきの方が、誤差によるばらつきよりも大きいことは視覚的には明らかですが、実際には、F検定という方法によって、要因の効果によるばらつきと誤差によるばらつきの比に有意差があるかを数値的に確認します。
分散分析では複数の要因について、どの要因に効果があるか、また要因同士の交互作用も知ることが出来ます。
４．最適水準の決定
分散分析の結果から、効果のある要因が求められた場合、要因のどの水準において特性値が最大になるか、最適水準を求めます。この最適水準が、この実験で求めたかった値となります。
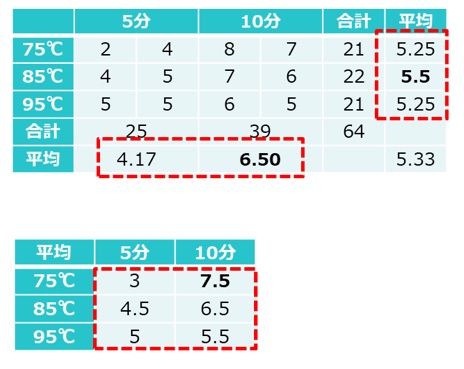
実験で得られた結果が右表のようなものであり、交互作用がないと判断される場合には、それぞれの因子の水準ごとの平均を比較して最大となる水準を選びます。この場合、最適水準は85℃・10分となります。
一方、交互作用があると判断される場合には因子を別々に考えるのではなく、各組み合わせにおいて最大となる水準の組み合わせが最適水準になります。この場合、最適水準は75℃・10分です。
【図4 最適水準の検討】
このように、交互作用の有無によって、最適水準や母平均の推定方法も変わってくるため、交互作用があると考えられる場合は注意が必要です。
５．適切な解析のために
ここまでの当連載コラムでは、実験計画法の基本知識と原則を、簡単な例に基づいて説明してきました。
コラムで取り上げた実験例の程度の規模なら、実験計画法などと大げさに考えなくても正しい結論に到達できると考えられるかもしれませんが、因子数や水準数、繰り返し数が増えると、実際の解析は加工された数値（平均値など）だけを見てやることになります。すると、たとえば今回の最適水準の決定の項で説明した実験例で、交互作用を考えずに平均値だけを見れば、「時間は長い方がよさそうだ（4.17と6.50の比較）、温度はまああまり影響はないかな（5.25と5.5の比較）」という結論になる可能性があります。
しかし本当は、交互作用まできちんと見れば、最適条件を見つけるためにはさらに低温で長時間の実験をやってみよう、という方向に行くはずです。
適切な解析ができるようにするには、実験計画段階で実験条件をどう選ぶか、得られた結果を正しく解釈しているか、が大切です。
（日本アイアール株式会社 H・N)
