《実験の手順》要因配置実験と直交配列表実験のポイント

Tweet

Pocket

当連載コラムの第３回までで、実験計画法で用いる概念や言葉の説明を通じて、実験計画法ではどのように考え、どのように実験を行うのかを示しました。

今回からはもう少し具体的に、実験の手順について説明します。

１．実験の手順

実験計画法に則った実験では、どのような要因によって特性に影響が出るか、要因をどのような値に設定するのが良いか明らかにするために、一般的に図のような流れで行います。

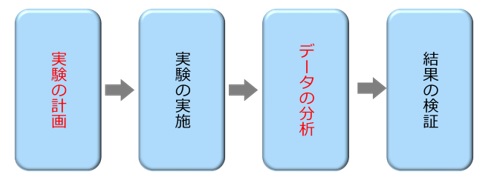
【図1　実験の手順】

以下では、実験計画法で重要となる「実験の計画」「データの分析」を中心に詳しく説明していきます。

２．実験の計画と実施

実験の計画と実施は、以下のように行います。

《実験の計画》

1. 実験の目的を明確にし、特性値を設定します。
2. 特性に影響を与える因子を選定します。（例：特性要因図など）
3. 水準を設定します。
4. 明らかにしたい要因効果を決め、適用する方法を決定します。（例：要因配置実験、部分配置実験など）

 
《実験の実施》

1. 実験は、実験計画法の原則に従ってランダムな順序で行います。
2. データを取得します。

この手順の中から、重要なポイントをいくつか解説します。

（1）特性に影響を与える因子の選定［特性要因図の作成］

実験を計画するにあたって、特性に影響を与えると考えられる因子を選定するために、特性要因図を用いることがあります。

特性要因図は、結果である特性と要因の関係を視覚的にまとめ明確化したもので、問題点の原因を調べたり、改善方法を発見するために用いられます。図のように魚の骨のようにも見えるため、「フィッシュボーン・ダイアグラム」とも呼ばれています。

特性要因図は、特性を決定し背骨を記入し、特性に影響を与える要因の大骨を作成します。要因については［Man：人、Machine：機械、Material：材料、Method：方法］の4Mで考えるとわかりやすくなります。そして大骨の要因に対して要因を追求し、中骨、小骨を記入していきます。
このようにして書き出した要因の中から、特性に大きく影響を与えると考えられる要因を因子として抽出します。

［※関連記事：QC七つ道具の基本④ 特性要因図とは？ はこちら］

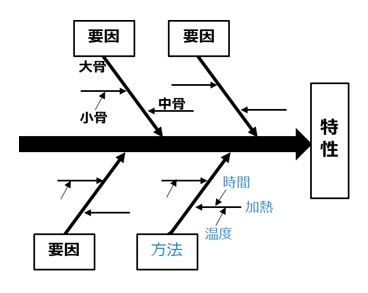
【図2　特性要因図】

（2）適用する方法の決定［実験計画法の種類について］

実験計画法といっても様々な種類がありますが、組み合わせや順序の観点から分類すると次のような方法があります。

 
《組み合わせ》

1. 要因配置実験： 取り上げた因子と水準のすべてを実施する実験（総当たり）
   （例）一元配置実験、二元配置実験、多元配置実験
2. 部分配置実験： 一部の組み合わせでしか実施しない実験
   （例）直交配列表実験

 
《順序》

1. 完全ランダム法（完全無作為法）： 因子、水準、組合せを完全ランダムに行う実験
2. 乱塊法： ブロックの中で実験順序をランダムに決めて行う実験
3. 分割法： 1つの因子の水準を固定し、何段階かに分けて行う実験

これらの方法についてポイントを解説していきます。

３．要因配置実験の基礎知識

実験計画法の種類のうち、ここでは要因配置実験について説明します。

（1）一元配置実験

「一元配置実験」とは、1つの因子を取り上げて、特性に影響を及ぼすか調べる際に行う実験です。因子の水準を変更した時に、各因子が特性に与えると考えられる影響について統計的に有意な差があるか調べます。

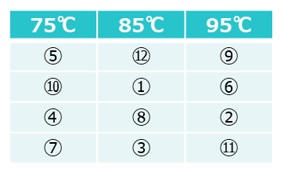
• 因子（表1の場合は温度）を1つとりあげて、その効果を調べる場合に使用
• 各水準で繰り返し実験が必要　(表1の場合、①→⑫のように3水準についてそれぞれ4回ずつ計12回をランダムな順序で実施）
• 要因効果を分散分析により検定

【表1　一元配置実験】

特性に影響を与える要因の調査をして、要因が絞り込まれた際に、その要因が及ぼす影響を調べる場合などに利用されます。一元配置実験は1因子での実験のため、交互作用は考えません。

（2）二元配置実験

「二元配置実験」とは、2つの因子を取り上げて水準を設定し、各水準の組み合わせで行う実験です。2つの因子を取り上げるため、交互作用があるかどうか見極めることが必要になります。

繰り返しのない二元配置実験

• 交互作用がないとわかっている場合に使用

繰り返しのある二元配置実験

• 因子を二つ（表2の場合、温度と時間）とりあげて、主効果と交互作用を調べる場合に使用
• 各水準の組み合わせで繰り返し実験が必要
  （表2の場合、①→⑫のように6つの組み合わせを2回ずつ、計12回をランダムな順序で実施）

【表2　二元配置実験（繰り返しあり）】

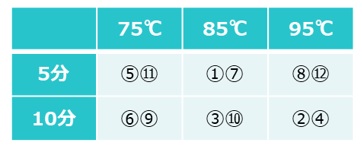
交互作用がある場合、繰り返しの実験を行わないと、交互作用を誤差と分離することができません（交絡）。
交互作用が誤差の中に含まれてしまいますし、主効果の検出精度も下がります。

（3）多元配置実験

「多元配置実験」とは、3つ以上の因子を取り上げて水準を設定し、各水準の組み合わせで行う実験です。

• 因子を3つ以上とりあげて、主効果と交互作用を調べる場合に使用
• 三元配置実験では・・
  実験の繰り返しがない場合（表3）は①→⑫のようにランダムな順序で実施し、主効果と2因子間の交互作用を検出する
  実験の繰り返しがある場合は3因子間の交互作用も検出可となる
• 要因効果（主効果、交互作用）を分散分析により検定

一般的に3因子間以上の交互作用は考えないことが多く、実験回数が多くなることから多元配置実験では繰り返しを行わないこともあります。

【表3　三元配置実験（繰り返しなし）】

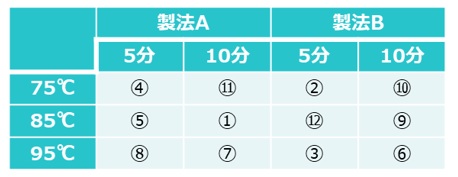
（4）要因配置実験のまとめ

ここまで、要因配置実験を簡単に説明してきました。
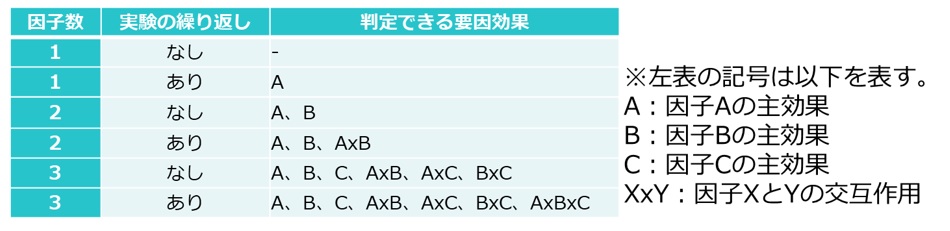
要因配置実験の因子と繰り返しの有無によって、分散分析で判定できる要因効果を表4にまとめました。

【表4　要因配置実験まとめ】

多元配置実験ではあまりにも実験数が多くなる場合、次回に説明する直交配列表実験を行うことも考えます。
要因配置実験のようにすべての交互作用を検出することは狙わず、取り上げたい交互作用だけを選別することで実験数を減らすこともできます。

４．直交配列表実験の基礎知識

部分配置実験の代表である「直交配列表実験」について説明します。

多数の因子の組み合わせをすべておこなう要因配置実験の場合、
　[2水準3因子] 　2³=8通り
　[2水準4因子]　 2⁴=16通り
このくらいの数であれば、現実的な実験として行えそうです。
しかし因子数が多くなると、例えば[2水準7因子]では 2⁷=128通りと大変な数です。

そこですべての水準組み合わせを実験するのではなく、一部の水準組み合わせのみを実験するのが「部分配置実験」です。どの水準組み合わせで実験するのかを決めることが重要になります。

部分配置実験の一種である「直交配列表実験」は、直交配列表（直交表）を利用して、少ない実験回数で各因子の効果や因子間の交互作用の効果を測定できるようにした方法です。
つまり、実験回数を減らす際に、どのような組合せで実験すれば良いかを教えてくれるツールが直交配列表であるということになります。
2水準系直交配列表(2ⁿ系)や3水準系直交配列表(3ⁿ系)など水準数により様々な直交表があります。

直交表の例と使い方

最も単純な例として、表5のように３因子についてそれぞれ２水準を取って実験する場合に、直交配列表を適用してみましょう。因子間に交互作用はないものとします。

【表5　３因子２水準実験】

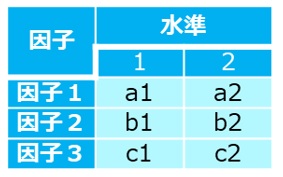
これを2水準多元配置実験として行う場合、2³=8通りの総当たりとなります。

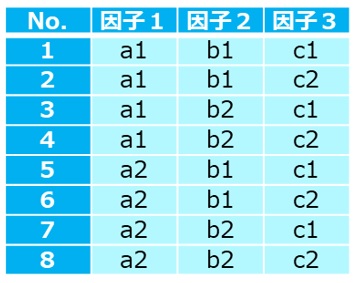
【表6　総当たり実験での因子水準の組み合わせ】

ここで表7の直交表を用いると4通りの実験ですが、8通りの多元配置実験と同等の情報を得ることができます。
これは、直交表では、それぞれの因子の列の各水準の中に他の列の各水準が同回数ずつ現れるように作られているからです。

例えば表7の因子１がa1水準であった場合（実験No.が１と２）、因子２についてはb1、b2が１回ずつ、因子３についてもc1、c2が１回ずつ出てきますので、実験No.１と２の平均値をとれば、因子間に交互作用がない場合、因子２と因子３の効果は相殺されて因子１の効果だけが残ることになります。
因子２、因子３についても同様に言えることを表7で確認して下さい。

【表7　直交表実験での因子水準の組み合わせ】

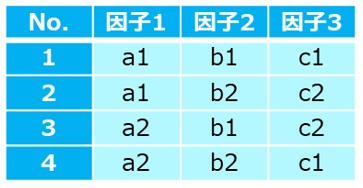
表7を示すのに、一般的には下記のような表記方法を使います。

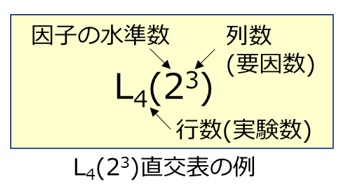
効果があるかどうかわからない因子について、交互作用まで含めて効果の有無を調べようとすれば、多くの因子の組み合わせで実験を行う必要が出てきますが2水準系直交表はL4、L8、L16・・、 3水準系ではL9、L27・・などがあり、例えばL₈(2⁷) 直交表を用いれば2水準、最大7要因まで適用でき、2⁷=128通りの組み合わせが8通りで確認できます。

次回は、実験の順序（乱塊法と分割法）を解説します。

（日本アイアール株式会社　H・N)

Tweet

Pocket