【電気数学をシンプルに】複素数をベクトルで表記する方法
本コラムでは、複素数 Z=a+jb（a、bは実数、jは虚数）をベクトルで表記する方法について解説します。
１．複素数をベクトルで表記する方法
（1）直交座標表示
「直交座標表示」とは、互いに直交する座標軸を決めて座標を表す方法です。
例えば、図1左のように、横軸xと縦軸yで表されるxy平面において、点(a, b)を表す場合が直交座標表示になります。この場合、xとyの値が決まれば点(x, y)は一意に定まるので、机上で検討する際には便利な表示方法になります。
複素数Zは、図1右に示したように、互いに直交する実軸Re、虚軸Imから成る複素平面（ガウス平面）上にベクトルとして表すことができます。
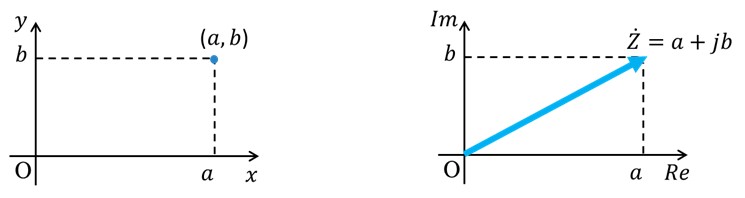
［図1 直交座標表示］
（2）極座標表示
「極座標表示」とは、固定点である極からの距離（動径）rと、極から出る直線（始線）と動径rとのなす角θ（偏角）を用いて点(r, θ)を表す方法になります。
例えば、円座標での表示は極座標表示の一種です。2次元の平面であるxy平面においては、原点を極として、始線をx軸とした場合には、図2左に示すように、原点からの距離が動径rになります。
偏角θは始線から反時計回りに考えます。
極座標表示では、図2右に示したように、複素数Zを複素平面上にベクトルとして表したとき、ベクトルの大きさとベクトルと実軸とのなす偏角θの値で表すことができます。
なお、ベクトルの大きさ|Z|は、三平方の定理より
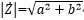
になります。
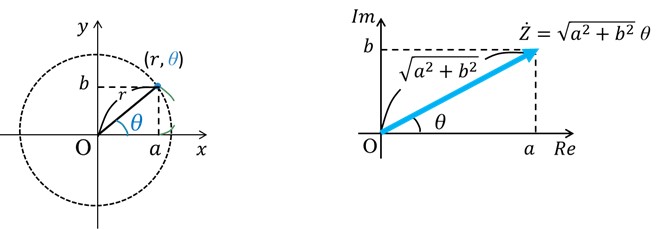
［図2 極座標表示］
ここで、
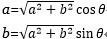
であることから、極座標を直交座標に変換できることがわかります。また、
b/a=tanθであるから、θ=tan-1b/a
となり、直交座標を極座標に変換することもできます。
極座標表示は、直感的に物理現象を表す際に適した方法です。
（3）三角関数表示
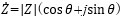
直交座標表示と極座標表示を変換する際にも三角関数を用いましたが、図3に示したように、複素数Zは、三角関数を使ってベクトルで表すこともできます。
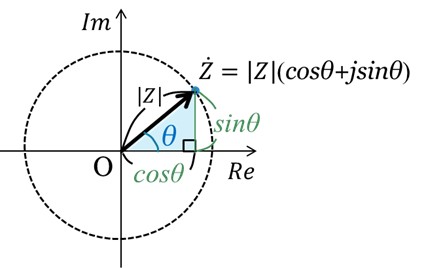
［図3 三角関数表示］
（4）指数関数表示
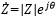
三角関数表示 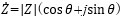は、オイラーの公式を用いると指数関数で表すこともできます。
［※オイラーの公式については、「オイラーの公式と交流電圧」のページをご覧ください。］
２．複素数を計算する工夫を
以上のように複素数をベクトルで表す方法は、4種類あります。
場面により表示方法が異なりますが、同じことを意味している点に注意が必要です。
また、表示方法を変換するだけで計算が簡単になるので、本コラムの内容を思い出して工夫してみましょう。
（日本アイアール株式会社 N・S)
