【早わかりポンプ】ターボ形ポンプの揚水原理(速度三角形とオイラーヘッド)

これまで当連載では、ターボ形ポンプに関する数々のコラムを書いてきました。
今回は、そもそもターボ形ポンプがいかにして流体にエネルギーを付与することができるのか、その基本原理について解説いたします。
1.速度三角形
ターボ形ポンプの一種である遠心ポンプの羽根車を正面から見ると、図1のように羽根翼は羽根車の回転方向に対して後向きに湾曲した形状をしています。
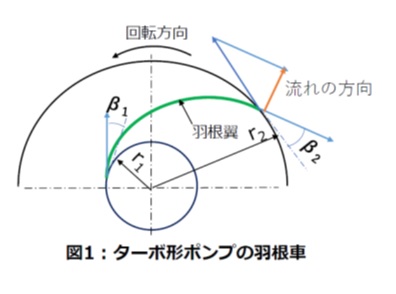
羽根翼の出口における接線と円周方向との間の角度を出口角β2、翼の入口における接線と円周方向との間の角度を入口角β1といいます。
羽根車出口から流出する流体の絶対速度をv2、入り口から流入する流体の絶対速度をv1とします。
羽根車出口半径をr2、入り口半径をr1、角速度をωとすれば、翼の先端部は周方向に出入り口でそれぞれ u2=r2ω、u1=r1ω の速度成分を有します。これを出口周速度、入り口周速度といいます。
流体は翼の入口角β1に沿って流入し、出口角β2に沿って流出します。
したがって回転座標系からみたとき、流体は翼角と一致した方向の速度成分を持ちます。
これを出口相対速度w2、入り口相対速度w1といいます。
固定座標系から見たときの実際の流入流出速度は、周速度uと相対速度w、および翼角βから描かれる三角形から求めることができます。この三角形のことを「速度三角形」といいます。
図2は出口における速度三角形です。
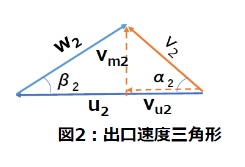
固定座標系から見た実際の流体の速度のことを、それぞれ出口絶対速度v2、入り口絶対速度v1といいます。
速度三角形において、絶対速度ベクトルと周速度ベクトルのなす角度を、入り口側α1、出口側α2とします。
また絶対速度のメリディアン(子午面)成分にm、周方向成分にuの添字をつけて表すこととします。
2.角運動量の法則とオイラーヘッド
羽根車が流体にエネルギーを与えることが出来るのは、どのような理論に基づくものなのでしょうか。
羽根車の作用のベースとなるのは運動量の法則です。
質量mの物体が、速度vで運動しているとき、
運動量 M = mv ・・・ (1)
速度の1回微分は加速度になるので、運動量の時間的な変化割合は、その物体に及ぼす力に等しくなります。
すなわち、
F = ma = m dv/dt = d/dt(mv) = dM/dt ・・・ (2)
で、この(2)式を「運動量の法則」といいます。
ある質量の集合体が半径rで回転するとき、
rF = d/dt(rmv) ・・・ (3)
(3)式左辺は回転中心に対する力のモーメントT、右辺のrmvは、回転中心に対する運動量のモーメント、すなわち角運動量Lとなります。
角運動量の時間的変化は、質点に及ぼす力のモーメント、すなわちトルクに等しくなります。これを「角運動量の法則」といい、質点の集合体とみなすことができる連続体の流体要素にも適用することができます。
角運動量の法則より、流体が羽根車を通過する間に発生する角運動量の変化は、流体に与えられたトルクTに等しくなります。
流体の密度をρ[kg/m3]、流量をQ[m3/s]とすれば、
T = ρQ(r2v2cosα2-r1v1cosα1) = ρQ(r2vu2-r1vu1) ・・・ (4)
ここで、vu2、vu1は、羽根車出口・入口における絶対速度の周方向成分です。
羽根車はトルクT[Nm]に対抗して角速度ω[rad/s]で回転するので、P=Tω[Nm/s]は羽根車を駆動するための動力となります。
周速 u=rω ですから、(4)式より
P = Tω = ρQ(ωr2vu2-ωr1vu1) = ρQ(u2vu2-u1vu1) ・・・ (5)
Pは流量Qの流体に与えられる動力(単位時間当たりの仕事)を表します。
一方、単位時間⊿tに質量mの流体の位置エネルギーを Hth∞[m] に相当する分だけ増加させるため必要な動力Pthは、
Pth = mg Hth∞/⊿t = ρgQ Hth∞ ・・・ (6)
Pthは、羽根車を駆動する動力Pに等しくなるので、(5)、(6)式より
Hth∞ = Tω/ρgQ=(1/g )(u2vu2-u1vu1) ・・・ (7)
これは、損失が全く無いとした理想的な状態で出し得るポンプ理論揚程を表すもので、「オイラーヘッド」と呼ばれます。
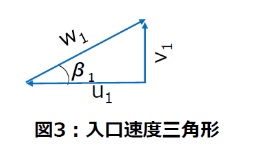
遠心羽根車の場合、通常は流体が旋回成分を持たずに真っすぐに羽根車に流入するので、周方向速度成分vu1=0とみなすことができます。すなわち入口速度三角形は図3のような直角三角形となります。この場合オイラーヘッドは
Hth∞ = (1/g )(u2vu2) ・・・ (8)
絶対速度v2のメリディアン(子午面)成分をvm2とすれば、速度三角形から(8)式を(9)式のように表すことができます。
Hth∞ = {u2(u2-vm2cotβ2}/g ・・・ (9)
3.速度三角形とオイラーヘッド
速度三角形で、余弦定理により次の関係が成り立ちます。
uvu = uvcosα = (u2+v2-w2)/2 ・・・ (10)
(10)式を用いて、オイラーの式(7)を書き替えると次のようになります。
Hth∞ = (v22-v12)/2g+(u22-u12)/2g+(w12-w22)/2g ・・・ (11)
第1項は速度エネルギーの増加(絶対速度の増加)を、第2項と第3項は圧力エネルギーの増加を、それぞれ表します。
圧力エネルギーのうち第2項は遠心力による効果、第3項は減速効果(デイフューザ)による圧力増加であり、3つの速度成分のうち、相対速度のみは羽根入口側の方が羽根出口側より大きく羽根車内部で減速する形となります。
ターボ形ポンプのうちの遠心ポンプは、第2項の周速度増分が支配的となります。羽根車外径を大きくするほど周速度の差が大きくなるので、それだけ高い揚程を得ることができます。これが「遠心ポンプ」と呼ばれる所以です。
それに対し、軸流ポンプの場合は、入口出口の羽根径が同じですから第2項の周速度増分はゼロとなり、第3項の相対速度減速で発生する揚力を利用します。また渦巻きケーシングや案内羽根は、第1項の絶対速度の増加分を効率的に減速させて圧力に変換する役割を担います。
4.実際のポンプ特性
(1)すべりの影響
オイラーの揚程は、翼枚数が無限で羽根の厚みもないとした仮想の羽根車で損失が全く無い理想的な状態における理論揚程を表す式です。
実際には、羽根翼は有限枚数で、翼は厚みを持っているので、流れにすべりが生じて、揚程はオイラーヘッドよりも低下します。
すべり係数をkとおけば、より実際的な理論揚程は(9)式にすべりを考慮して
Hth = [u2{u2(1-k)-vm2cotβ2}]/g ・・・ (12)
ここで流量Q/羽根車出口面積 A = vm2 であることから、メリディアン流速 vm2 は流量に比例して変化する量です。
したがって、理論揚程の特性曲線は図4のように
流量ゼロ(vm2 =0)における揚程 = u2(u2(1-k)/g から、出口角度β2に依存した勾配で、流量増加とともに揚程が低下する右下がりの直線となります。

(2)水力損失の影響
羽根車内部で発生する流れの衝突や、流れと流路壁面との摩擦により発生する損失のことを「水力損失」といいます。
摩擦損失は管路損失と同様に、流量の2乗に比例して増大するので K1Q2 の形で表すことができます。
衝突損失は羽根車内部の流れの向きが、羽根車の角度と合致せず流れが衝突することにより発生する損失であり、K2(Qs-Q)2の形で表すことができます。
ここでQsは「無衝突流量」といい、通常は最高効率点流量より20~30%程度大流量側となります。
水力損失 hL = K1Q2 + K2|Qs-Q|2 ・・・ (13)
(11)式の理論揚程から(12)式の水力損失を引いた結果、ポンプの流量‐全揚程特性は図5の1点鎖線で示す曲線となります。
(3)漏れ損失の影響
羽根車が回転するためにケーシングとの間にすき間を設ける必要があります。
すき間部の前後には羽根車による昇圧で発生する差圧があるので、すき間を通過する漏れ量qが生じます。
1点鎖線の特性 H = Hth-hL から漏れ量qを引いた結果結果、実際に得られる(測定される)ポンプの流量‐全揚程特性(QHカーブは)図5の実線で示すような曲線となります。
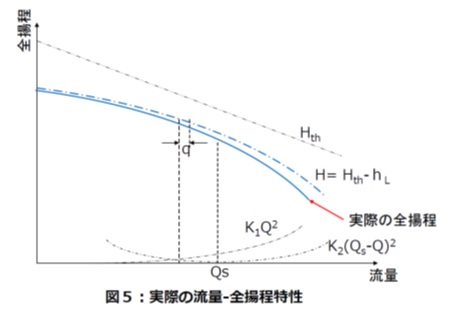
つまり、ポンプのQHカーブとは、理論揚程オイラーヘッドから、すべりと各種の損失を引いた結果得られるポンプの特性である、ということができます。
(日本アイアール株式会社 特許調査部 S・Y)