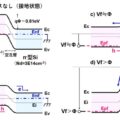
【電気数学をシンプルに】複素数の計算方法(四則演算と共役複素数)
交流回路を解析して計算していくためには複素数を用いると便利です。
本コラムでは、複素数を計算する方法について解説します。
1.複素数の四則演算
複素数Z1=a+jb (a、bは実数、jは虚数)、複素数Z2=c+jd (c、dは実数、jは虚数)とします。
(1)複素数の加算
複素数の加算は、実部と虚部に分けて計算を行います。
図1のように、ベクトルの和で考えるとわかりやすいかもしれません。
Z1+Z2=(a+jb)+(c+jd)
=a+c+j(b+d)
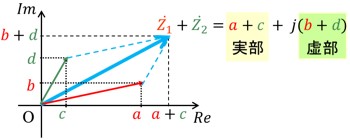
[図1 ベクトルZ1とベクトルZ2の和]
(2)複素数の減算
複素数の減算も、加算と同様に実部と虚部に分けて計算を行います。
図2はベクトルの差を示しています。
ベクトルの差は、向きを逆にしたベクトルの和として考えることができます。
Z1-Z2=(a+jb)-(c+jd)
=a-c+j(b-d)
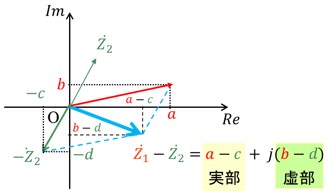
[図2 ベクトルZ1とベクトルZ2の差]
(3)複素数の乗算
複素数の乗算は、多項式を展開するときと同じように計算していきます。
虚数の定義より、j2=-1になります。
Z1Z2=(a+jb)(c+jd)
=ac+jda+jbc+j2bd
=(ac-bd)+j(da+bc)
(4)複素数の除算
複素数の除算は、共役複素数を使って分母を実数化します。分母である複素数Z2=c+jd の共役複素数は、![]() =c-jdです。
=c-jdです。
分母と分子に共役複素数をかけることで、分母の虚数をなくしています。
(※共役複素数については、後述します。)
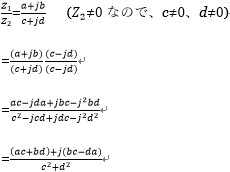
以上のように、複素数に四則演算を施しても、その結果はまた複素数になることがわかります。
2.共役複素数
複素数Z=a+jb (a、bは実数、jは虚数)と対になる複素数![]() =a-jbを「共役複素数」といいます。
=a-jbを「共役複素数」といいます。
図3のように、複素平面(ガウス平面)上にベクトルとして表すと、複素数Zは、共役複素数![]() と実軸Reに関して対称になります。
と実軸Reに関して対称になります。
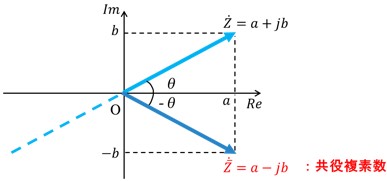
[図3 複素平面上における複素数Zと共役複素数![]() ]
]
複素数Zは、共役複素数![]() をかけると、
をかけると、
Z![]() =(a+jb)(a-jb)
=(a+jb)(a-jb)
=a2-jab+jba-j2b2
=a2+b2
となります。
また、複素数Zの大きさ|Z|と共役複素数|![]() |は等しく、
|は等しく、
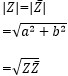
になります。
なお、複素数の四則演算では、複素共役をとってから四則演算をする場合と、四則演算をしてから複素共役をとる場合とで、結果が等しくなります。
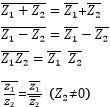
【問題】共役複素数を使った電流の計算
RLC直列回路(図4)において、R=8[Ω]、誘導リアクタンス![]() =10[Ω]、容量リアクタンス
=10[Ω]、容量リアクタンス![]() =4[Ω]、回路全体の電圧
=4[Ω]、回路全体の電圧![]() =100[V]のとき、電流
=100[V]のとき、電流![]() を求めてみましょう。
を求めてみましょう。
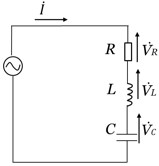
[図4 RLC直列回路]
《解答》
《解説》
以上のような問題を繰り返すことで、複素数の計算方法を身につけて頂ければと思います。
(日本アイアール株式会社 N・S)



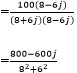











](https://engineer-education.com/wp/wp-content/uploads/2021/10/electric-circuit-dc0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2021/10/Circuit-element0-150x150.png)