【電気数学をシンプルに】電気数学とは?初心者が押さえておくべき前提知識を解説

1.電気数学とは?
電気数学とは、電気工学や電磁気学の問題を解くときに使う数学だったり、電気を知るために用いる数学と受け止められることが多いようですが、本連載コラムでは、電気回路・電子回路をよりわかりやすくするための数学と捉えて解説していきます。
電気数学が、電気工学等と数学の間に位置する内容であることは想定できると思いますが、あくまで電気よりの視点で書いています。
まず今回は、電気数学の中心となる、三角関数・ベクトル・複素数の前提知識をチェックしてみましょう。
電気の様子を説明するために数学の知識が必要?
電気には、直流と交流があります。
その様子を説明するために可視化する際は、数学で習うようなグラフを描く必要があります。
図1は、直流と交流における電流・電圧の時間変化を表したグラフです。
一般に左のグラフが直流で、右のグラフが交流を表しています。(電流の流れる方向が一定であれば、電圧・電流が変化するものを直流と扱う場合もあります。)
交流は、電流・電圧が周期的に変化する電気であり、家庭用コンセントに代表されるような商用電源は交流です。そして、交流の多くは正弦波交流であり、右のグラフのように横軸に時間、縦軸に電圧または電流をとると、サインカーブ(正弦曲線)になります。

[図1 直流と交流のグラフ(左が直流、右が交流)]
2.電気数学で重要となる三大前提知識
(1)三角関数
電気数学で扱う三角関数は、三角比と呼ばれる鋭角である直角三角形の二辺の長さの比です。
sinθ、cosθ、tanθで表され、図2に示すθ=30°、45°、60°の場合においては、暗記されている方も多いと思います。
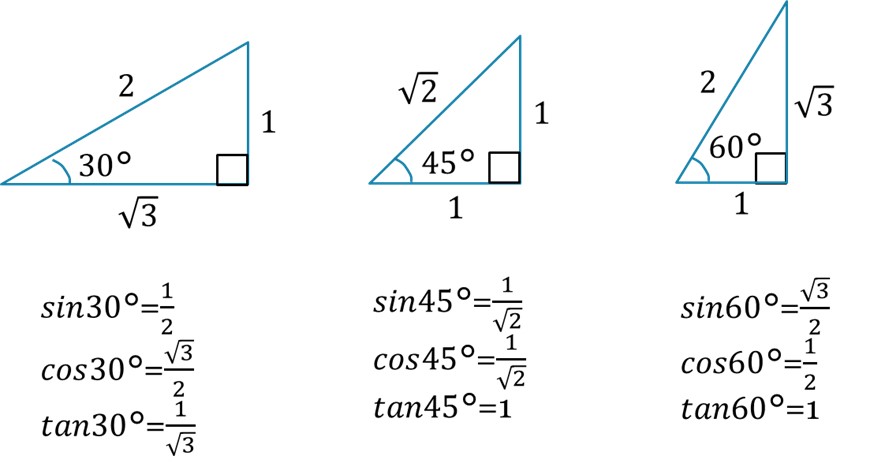
[図2 よく使われる三角比]
先にも述べた通り、交流はほとんどがサインカーブで表される正弦波交流なので、波形解析をする際には三角関数の知識が不可欠です。
(2)ベクトル
ベクトルは、「大きさ」と「向き」という2つの情報を含んだ量です。
「大きさ」のみの量は、「スカラ」といいます。
例えば、Aと記載されている場合にはAはスカラであり、ベクトルの場合には、![]() (または
(または![]() )と書き、ベクトルAと読みます。図3に示されるように、図面上では矢印で表現されます。
)と書き、ベクトルAと読みます。図3に示されるように、図面上では矢印で表現されます。
ベクトルが始まる位置を始点、終わる位置を終点といいます。
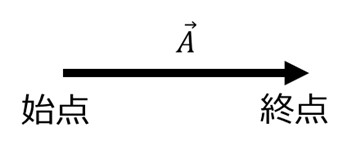
[図3 ベクトルの例]
図4の左側に示したように、xy平面上で、![]() を原点Oを中心に反時計周りに回転させると、
を原点Oを中心に反時計周りに回転させると、![]() の終点は円上を移動します。つまり、円運動をします。
の終点は円上を移動します。つまり、円運動をします。
また、図4の右側には、このときの![]() の終点の軌跡を、横軸にx軸との角度、縦軸にyの値としてプロットしています。
の終点の軌跡を、横軸にx軸との角度、縦軸にyの値としてプロットしています。
ここで、![]() 終点の軌跡が図1に示した交流のグラフと同じく正弦波になることがわかります。
終点の軌跡が図1に示した交流のグラフと同じく正弦波になることがわかります。
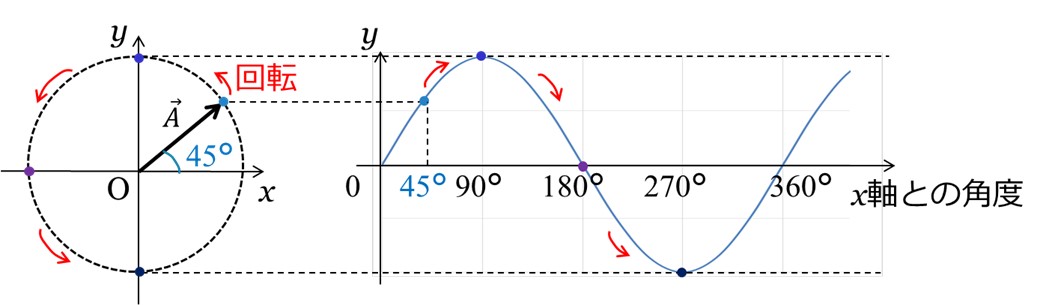
[図4 ベクトルと正弦波の対応]
このように、交流波形をベクトルとして考えることができます。
(3)複素数
複素数Zは、2つの実数a、bと虚数iを用いて表すことのできる数です。
Z=a+bi
aを「実部」(Real)、bを「虚部」(Imaginary)といいます。
ここで、虚数(Imaginary number)は、2乗したらマイナス1になる数として定義されています。
一般には頭文字であるiで表しますが、電気工学等においては、iが交流電流を表すため、区別できるようにjで表現します。
また、計算のしやすさから慣習として、bjではなくjbと記載されます。
Z=a+jb
図5のように、複素数Zは、横軸を実部Re、縦軸を虚部Imとした複素平面上において、ベクトルとして表すことができます。また、逆に複素数はベクトルを数式化したものといえます。
したがって、交流回路の計算は複素数を用いることで楽になるのです。
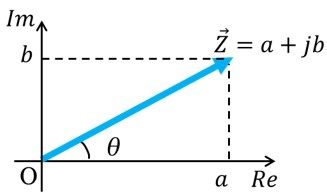
[図5 複素数Zのベクトル表示]
ということで、今回は電気数学を学んでいくうえで必須となる重要前提知識を簡単にご紹介しました。
今後の連載では、三角関数・ベクトル・複素数の関係について具体的に説明していきます。
次回は「ベクトルと位相・位相角」に関する解説です。
(日本アイアール株式会社 N・S)










](https://engineer-education.com/wp/wp-content/uploads/2021/10/electric-circuit-dc0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2021/10/Circuit-element0-150x150.png)
































