組み合わせ回路を基礎から学ぶ!マルチプレクサやデコーダの仕組みと回路例

1.デジタル回路の「組み合わせ回路」とは
デジタル回路は、「論理回路」とも呼ばれていますが、論理回路のうち入力信号の組み合わせだけで出力が決まるような論理回路を「組み合わせ回路」と呼びます。逆に、内部に記憶回路と同期回路を備え、入力信号の組み合わせだけで出力が決まらない論理回路を「順序回路」と呼びます。(※順序回路の解説記事はこちら)
今回は、前者の「組み合わせ回路」について説明します。
「組み合わせ回路」は、ANDやOR、NOT、XORなどの論理ゲートを複数個組み合わせることにより構成されます。数種類の論理ゲートを並べると、様々な機能が実現できます。
2.論理ゲート
論理ゲートとは、ANDやOR、NOT、XORなどのことを言います。
特にAND、OR、NOTの3種類を基本論理ゲートと呼びます。
ゲートについて、図1の回路図を用いて説明します。
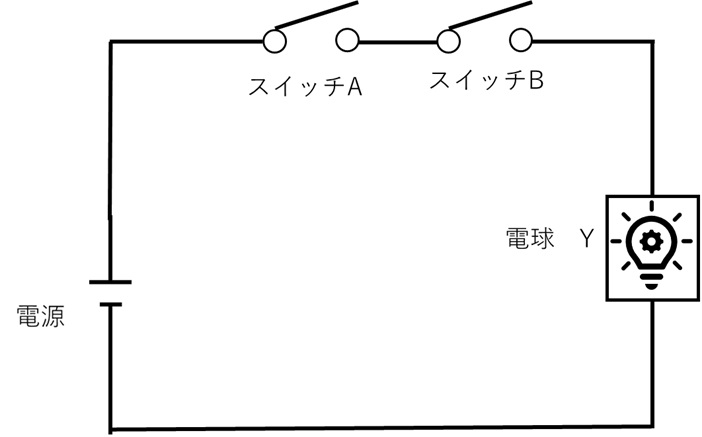
【図1 論理ゲートと回路図】
図1において、AかBのスイッチのどちらかを「オフ」に固定すると、電球Yは消灯したまま、つまり、出力が「オフ」に固定されることになります。これは、ゲートを閉じることを意味します。
逆に、AかBのスイッチのどちらかを「オン」に固定すると、固定していないもう一方の入力がそのまま出力に反映されることになります。これは、ゲートを開くことを意味します。
このようなゲートの考え方を利用しているものが「論理ゲート」となります。
3.組み合わせ回路の例(マルチプレクサなど)
組み合わせ回路の中には、「マルチプレクサ」や「デコーダ」などがあります。
以下、それぞれの回路について、簡単な例でご説明します。
(1)マルチプレクサ
「マルチプレクサ」とは、複数の入力信号から出力する信号を選択する信号切り替え器のことを言います。
例えば、2つの信号のどちらかを切り替えて出力するマルチプレクサを考えてみましょう。
図2は、そのマルチプレクサの回路を示した図です。
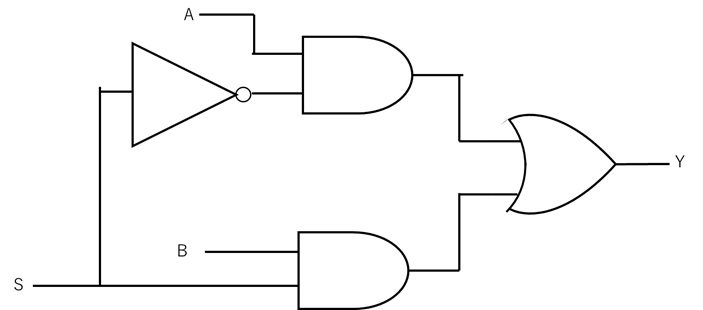
【図2 マルチプレクサの論理回路(例)】
図2において、入力はAとB、出力はYとし、Sは入力を切り替える制御端子とします。
AとBは、それぞれ、1か0を入力し、Sは、1か0で制御し、出力Yには、1か0が出力されます。
図3に、S、A、B、Yの取りうる場合を示した真理値表を示します。
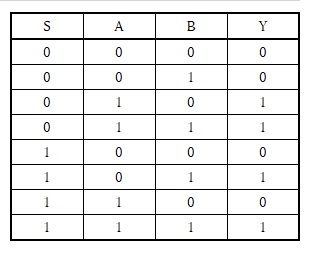
【図3 マルチプレクサと真理値表】
図2と図3より、Sが0の時は、Aが入力されているAND回路には、0を反転させた1が入力され、ゲートが開いて、Aの値が反映されます。
この時、Bが入力されているAND回路には、Sが0なので、ゲートが閉じていて、Bの値は、反映されません。
逆に、Sが1の時は、AのAND回路のゲートは閉じて、BのAND回路のゲートが開き、Bの値が反映されることになります。
図3のように、Sの入力次第で、出力Yに入力A、入力Bのどちらを反映させるのかが決まります。
すなわち、2つの入力信号から出力する信号をSによって選択していることがわかります。
このようにANDとORとNOTにより、マルチプレクサを実現できることになります。
上記の例では、Sが1系統なので(1か0)、2つの入力信号を制御するだけでしたが、Sを2系統、3系統と増やせば、4入力、8入力と制御できる信号の数を増やすことができます。
(2)デコーダ
デコーダは、入力を判定して該当する出力を1にする「組み合わせ回路」です。
AND回路とNOT回路の論理回路で表現すると図4のようになります。
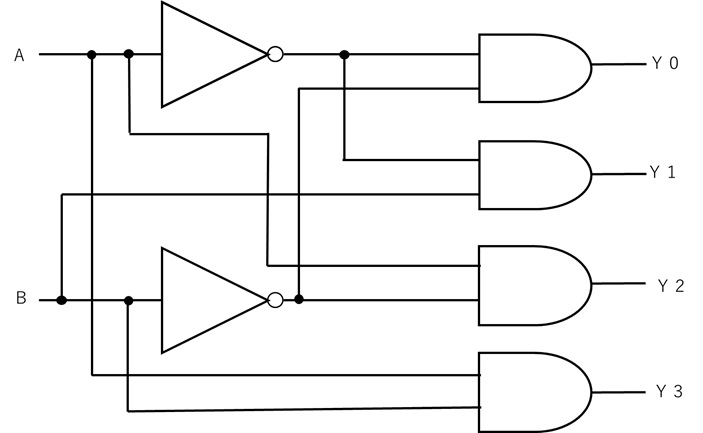
【図4 デコーダの論理回路(例)】
また、このデコーダの真理値表は図5となります。
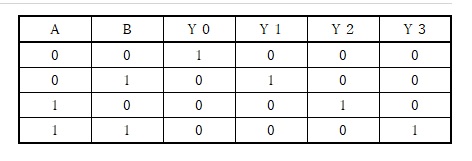
【図5 デコーダの真理値表】
この真理値表から2つの入力信号A、Bによって4つの出力信号(Y0、Y1、Y2、Y3)のいずれかに1が出力されることがわかります。
例えば、2つの入力を2進数に、4つの出力信号をそれぞれ10進数の0、1、2、3に対応させる(Y0を0、Y1を1、Y2を2、Y3を3)と考えると、2進数を10進数に復号化(デコード)している回路とみなすことができます。
以上、今回はマルチプレクサやデコーダについて紹介してきましたが、「組み合わせ回路」では、上記のように入力が決定すると出力は必ず1通りに定まります。
なお、デコーダについては「デジタル回路のエンコーダとデコーダ」の回でも解説していますので、ぜひ併せてご覧ください。
(日本アイアール株式会社 特許調査部 E・N)














](https://engineer-education.com/wp/wp-content/uploads/2021/10/electric-circuit-dc0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2021/10/Circuit-element0-150x150.png)
































