ヤング率とは?式と単位、横弾性係数との関係などを解説

当連載コラムの前回「フックの法則とは?」では、機械部材内部の応力とひずみの関係を考える上で重要となるフックの法則を解説しました。
今回は、応力とひずみの関係を表す比例定数である弾性係数について、もう少し詳しく見ていきます。
1.縦弾性係数「ヤング率」とは?
上記「フックの法則とは?」のコラムで記載した内容のおさらいですが、物体内部に比例限度以下の垂直応力σと縦ひずみεが生じるとき、
E = σ/ε ・・・(1)
Eを「縦弾性係数」または「ヤング率」(Young’s modulus)といいます(以下、「ヤング率」と表します)。
ヤングは、19世紀イギリスの物理学者トマス・ヤング(Thomas Young)に由来します。
(1)式において εは無次元数ですから、ヤング率の単位は応力と同じ[N/mm2](MPa)です。
ただし機械部品によく用いられる金属材料のヤング率の値は非常に大きいので、一般的には MPa ではなく GPa を用いる場合が多いようです。
| 金属材料の種類 | 単位[GPa] | |
| 一般構造用圧延用鋼材 | SS400 | 206 |
| 機械構造用炭素鋼 | S45C | 205 |
| クロムモリブデン鋼 | SCM435 | 205 |
| オーステナイトステンレス鋼 | SUS304 | 193 |
[主な金属材料(鋼材)のヤング率]
式(1)からわかるように、ヤング率が大きい材料ほど、応力が同じ場合のひすみが小さい、すなわち変形しにくい(剛性が高い)ということができます。
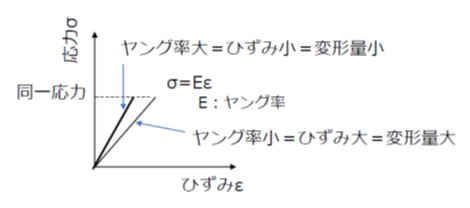
【図1 ヤング率とひずみ】
2.横弾性係数とは
垂直応力と縦ひずみの比例関係を示す定数としてヤング率(縦弾性係数)が定義されるのと同様にして、図2のように純せん断力を受ける物体に生じるせん断応力τとせん断ひずみγの比例関係が次式で定義されます。
G = τ/γ ・・・(2)
式(2)における比例定数Gを「横弾性係数」または「せん断弾性係数」といいます。
せん断ひずみは無次元数ですので、横弾性係数の単位も応力と同じ[N/mm2](MPa)であり、ヤング率と同様に通常 GPa を用いて表します。
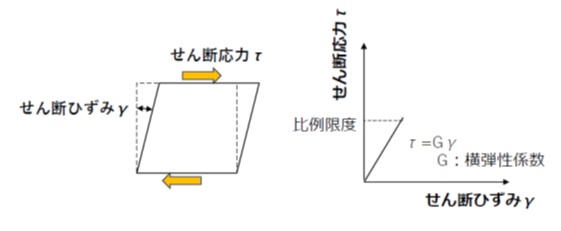
【図2 横弾性係数とは】
3.ヤング率、ポアソン比と横弾性係数の関係
図のように純せん断荷重を受ける場合であっても、見方を変える(座標軸を変える)ことにより、せん断荷重を引張と圧縮の垂直荷重に変換することができます。せん断応力τを垂直応力に変換した座標軸における、垂直応力の最大値、最小値のことを「主応力」といいます。
本コラムではその導出過程の説明は省略しますが、せん断応力を主応力(垂直応力)に変換することにより、横弾性係数Gとヤング率Eの関係を次式のように求めることができます。
E = 2G(1+ν) ・・・(3) (※ν(ニュー)はポアソン比)
[※関連記事:ポアソン比の基本はこれを読めばOK! はこちら]
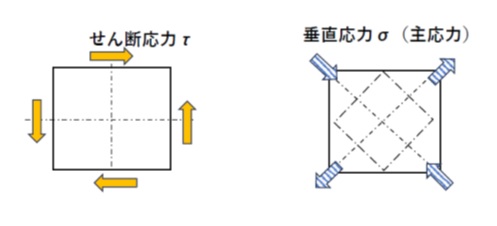
【図3 純せん断を受ける物体の主応力】
鉄鋼材料のポアソン比は0.3程度ですから式(3)より E≒2.6G
つまり、横弾性係数Gはヤング率Eの1/2より小さい値となります。
式(3)は、方向に関わらず機械的性質が変わらない等方性材料に対して適用されます。
機械部品によく用いられる金属や一般的な樹脂は等方性材料として扱うことができます。
以上、材料の応力とひずみの関係を考える上で重要となる「ヤング率」について解説しました。
弾性限度を超えた応力の領域における応力とひずみの関係については別途解説予定です。
[※関連記事:荷重、応力、ひずみの基本を整理!応力-ひずみ線図など重要知識をわかりやすく解説]
(アイアール技術者教育研究所 S・Y)
















](https://engineer-education.com/wp/wp-content/uploads/2019/06/facility_PM-150x150.png)