ひずみとは？ 縦ひずみ/横ひずみ、せん断ひずみの求め方、式・記号などを解説

Tweet

Pocket

当連載コラムの「応力とは？」では、機械設計を行うときの重要な指標となる応力について解説しました。
今回は、応力と密接な関係のある「ひずみ」についてお話ししたいと思います。

１．「ひずみ」とは？（ひずみの意味）

物体（機械部材）が外力（荷重）を受けると、部材内部に生じる応力によって変形が起こり、部材内部の各点は相対的に変位します。
機械の健全性を評価する上で、荷重の大きさではなく荷重によって部材内部に生じる応力が重要であるのと同様に、変形量そのものではなく、変形の健全性を絶対的に評価する指標が必要となります。
この指標が「ひずみ」（strain）であり、応力がゼロの状態における寸法（基準値）に対する、応力が生じたときの変形量の比率（変形の度合い）のことをいいます。

　ひずみ＝変形量[mm]/基準値[mm] 　　・・・（１）

すなわち、ひずみは単位を持たない無次元数です。

２．縦ひずみ、横ひずみ

図1の左のように、長さL[mm]、断面が直径D[mm]で一様な丸棒の左端を固定して、右端に棒の軸方向（縦方向）に荷重Fをかけて引っ張ったときに生じる棒の伸びをλ（ラムダ）[mm]とします。

荷重と同方向（縦方向）に生じる変形量の比率を「縦ひずみ」といいます。
縦ひずみを表す記号として ε（イプシロン）を使います。

（１）式における変形量がλ、基準値がLなので
　縦ひずみ ε = λ/L （引張力を受ける場合）　　・・・（２）　
となります。

一方、荷重と直交する断面方向（横方向）には縮みが生じて直径は減少します。
荷重と直交方向（横方向）に生じる変形量の比率を「横ひずみ」といいます。
引張力を受けたことに伴う直径の減少量を、δ（デルタ）とします。横ひずみを表す記号として ε’ を使います。直径減少のように、変形が基準値寸法を小さくする側に発生する場合は、ひずみは負（マイナス）記号をつけて表します。

したがって、次のようになります。
　横ひずみ ε’ = －δ/D （引張力を受ける場合）　　・・・（３）　

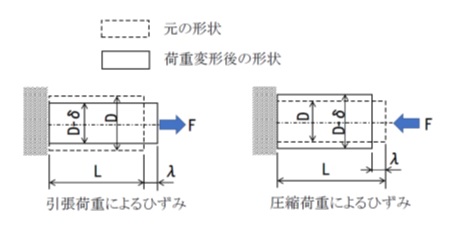
【図1　縦ひずみと横ひずみ】

次に図1の右のように、同じ長さL,直径Dの丸棒の左端を固定して、軸方向に引っ張るのではなく、押し付ける（圧縮する）方向の荷重を右端に加えた場合を考えます。

この場合は、圧縮されることで棒の長さは縮小し、逆に棒の直径は増大します。
したがって、縦ひずみと横ひずみは、引張力を受ける場合と正負が逆になります。

　縦ひずみ ε = ―λ/L （圧縮力を受ける場合）　　・・・（２）’
　横ひずみ ε’ = δ/D （圧縮力を受ける場合）　　・・・（３）’

３．せん断ひずみ

下図のように物体が、ある距離L離れた一組の面にせん断力Qを受ける場合に生じるひずみについて考えます。

せん断力Qにより、図のように物体に相対的なずれが生じたとします。その相対的なずれ量をλ（ラムダ）とします。また、ずれλが生じたことによって、せん断力の方向と直交する面（長さL）が回転した角度をα（アルファ）とします。

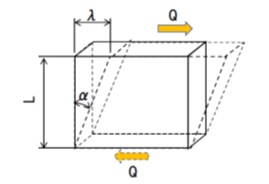
【図2　せん断力とせん断ひずみ】

せん断力を受ける物体に生じるひずみ（変形の度合い）のことを「せん断ひずみ」といい、γ（ガンマ）を用いて表します。

図の幾何学的関係より
　　γ = λ/L = tanα　・・・・・・・（４）
一般的に変形量（ずれ量）はごく小さいので tanα≒α とみなすことができます。

したがって　（４）式は
　　γ = λ/L ≒ α　・・・・・・・（４）’

すなわち、せん断ひずみγは物体の変形角度に等しくなります。

 
ということで今回は、荷重を受ける物体に生じる変形の度合いを表す「ひずみ」について解説しました。
前回のコラムで解説した応力とひずみの間には深いつながりがあります。ひずみを測定することにより、応力あるいは荷重を知ることができるなど、ひずみは工学的にも広く利用されています。

［※関連記事：荷重、応力、ひずみの基本を整理！応力-ひずみ線図など重要知識をわかりやすく解説］

次回のコラムでは、ひずみに関して押さえておくべき用語である「ポアソン比」を解説します。

（アイアール技術者教育研究所　S・Y）
 

Tweet

Pocket