【QC検定3級対策】相関分析の基本|相関係数の計算方法と判断基準など
QC検定は、JSA日本規格協会グループが主催する品質管理の知識を問う筆記試験です。
内容は品質管理とは何か?から始まり、改善活動の基礎知識、統計的なプロセス管理など多岐にわたります。
受験者数は年々増加しており、毎年の受験者数が10万人を超える製造業ではメジャーな試験です。
[※関連記事:【技術系資格ナビ】QC検定(1〜4級の難易度/合格率/勉強方法/メリット)はこちら]
この連載では、各級の頻出範囲について例題を交えて解説を行います。この連載を通じて、QC検定の受験準備をしてみましょう。
3級の試験範囲は日本規格協会のHP(品質管理検定レベル表)をご確認ください。
【3級解説:第7回】相関分析
今回は3級の試験範囲、手法分野の最終章「相関分析」について解説します。
(1)相関とは?
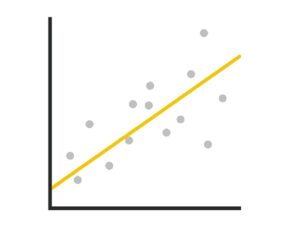
「相関」とは、散布図や相関係数などを用いて変数の関係を分析する方法です。
変数が2つ(xとy)の場合を「単相関分析」、3つ以上の変数の場合を「重相関分析」と言います。
QC検定3級では、単相関分析についてのみ取り上げられます。
(2)相関の種類
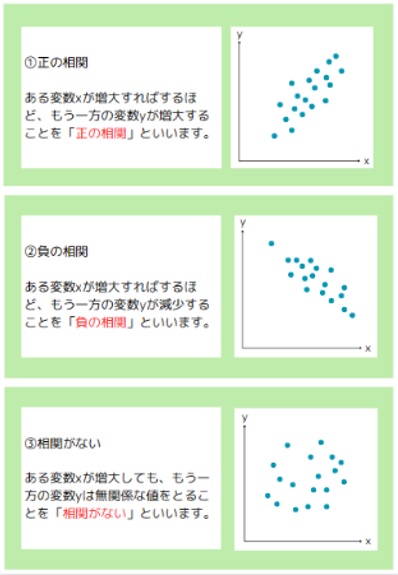
単相関分析では、ある変数xに対し、yがどのような値をとるかによって下記の3種類の相関関係があります。
- ① 正の相関: ある変数xが大きくなればなるほど、もう一方の変数yが大きくなる関係。
- ② 負の相関: ある変数xが大きくなればなるほど、もう一方の変数yが小さくなる関係。
- ③ 相関がない: ある変数xが大きくなっても、もう一方の変数yは無関係な値をとる関係。
(3)相関係数の計算方法(相関係数の求め方)
「相関係数」とは、2つの変数の間にどれだけ直線的な関係があるかを示した数値です。
一般的に「r」で示され、相関係数rは以下の式で計算します。nはデータ数です。
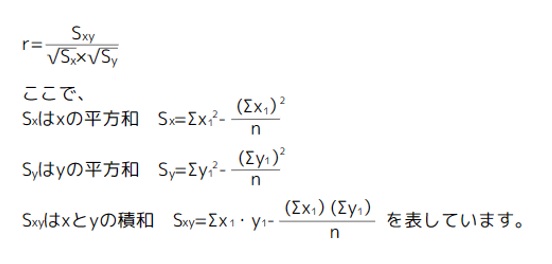
例として下記のデータから相関係数を求めてみましょう。
| 変数x | 変数y | |
| 1 | 2 | 4 |
| 2 | 3 | 5 |
| 3 | 6 | 11 |
| 4 | 7 | 15 |
| 5 | 9 | 18 |
まず以下のような計算補助表を作成します。
| x | y | x2 | y2 | x×y | |
| 1 | 2 | 4 | 4 | 16 | 8 |
| 2 | 3 | 5 | 9 | 25 | 15 |
| 3 | 6 | 11 | 36 | 121 | 66 |
| 4 | 7 | 15 | 49 | 225 | 105 |
| 5 | 9 | 18 | 81 | 324 | 162 |
| 合計 | 27 | 53 | 179 | 711 | 356 |
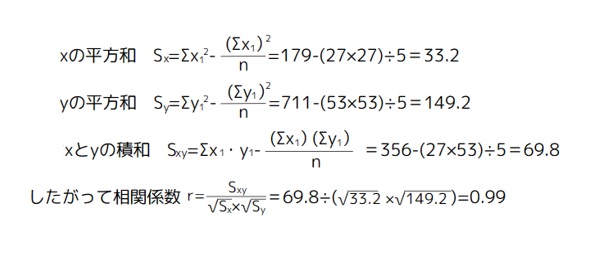
(4)相関係数の判断基準
相関係数の値からどの程度の相関があるかを判断できます。
※|r|は絶対値を示します。
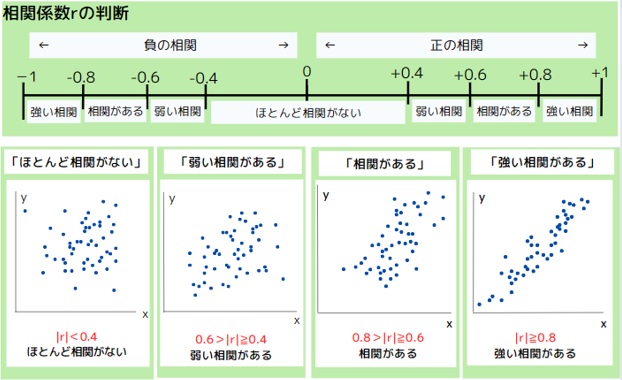
相関係数rは-1から+1までの値をとり、プラスの値をとるとき正の相関、マイナスの値をとるときは負の相関があることを示します。また、相関係数rが-1または+1に近い値をとるとき強い相関、逆に0に近い値をとるときはほとんど相関関係がないと言えます。
なお、相関係数は計算上の値なので、相関係数が限りなく±1に近くても変数の関係を推測しているだけで、因果関係を断定することは出来ません。また相関係数が0に近くても、直線関係にないだけで因果関係が全くないとは言えません。
QC検定3級の試験範囲外ではありますが、指数関数など直線関係以外の因果関係があるかもしれませんので注意しましょう。
それでは例題にチャレンジしてみましょう。
《例題1》
(1) 相関係数に関する次の文章について正しいものには〇を、正しくないものには×を記せ。
① 相関係数のとりうる値の範囲は-2≦r≦2である。
② 相関係数は2つの変数xとyの積和をxの平方和とyの平方和で割ることで求められる。
③ 2つの変数の値に対し相関係数rの値が0.97であるとき、「強い相関がある」と言える。
④ 2つの変数の値に対し相関係数が大きい値をとるとき、2つの変数の間には必ず相関関係があると言える。
⑤ 2つの変数の値に対し相関係数が0の場合は、両者にはまったく相関関係がないと言える。
《例題1》[解答と解説]
《例題2》
(1) 2つの変数xとyに関し下記のデータを取得した。このデータに関する相関係数の文章について( )内に入る言葉を下の選択肢から選べ。
| データ数 | 変数x | 変数y |
| 1 | 2 | 10 |
| 2 | 4 | 8 |
| 3 | 5 | 4 |
| 4 | 6 | 7 |
| 5 | 8 | 5 |
上記のデータの相関係数を求める。
・xの積和Sxは(①)
・yの積和Syは(②)
・xyの積和Sxyは(③)
したがって相関係数rは(④)である。
相関係数の値からこの変数xとyの間には負の(⑤)と言える。
選択肢
[ア.0.18 イ.5.8 ウ.7.4 エ.16.0 オ.20.0 カ.22.8 キ.-16.0 ク.-20.0 ケ.0.74 コ.-0.74
サ.相関がない シ.弱い相関がある ス.相関がある セ.強い相関がある]
《例題2》[解答と解説]
まとめ
以上、今回は相関分析について解説しました。
次回は、実践分野の中から品質の概念について解説します。
(アイアール技術者教育研究所 A・K)



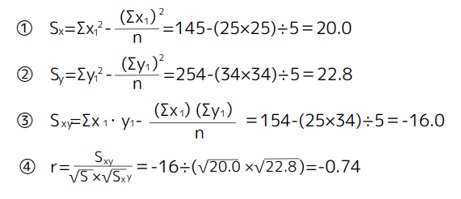












](https://engineer-education.com/wp/wp-content/uploads/2022/09/experimental-design_statistics_1-150x150.png)































