【パワー半導体の基礎】pn接合の整流作用とバンド図

Tweet

Pocket

pn接合ダイオードの整流作用^*1）は、半導体デバイスの最も重要な機能の一つです。
この記事では「整流作用のメカニズム」をエネルギー・バンド図（以下、バンド図）を用いて紹介します。

^*1） 「ダイオードの整流作用と電気特性」参照。

１．n型Siにおけるフェルミ・レベルEnfの位置

pn接合のバンド図を描くためには、先ず初めにp型Siとn型Siの「フェルミ・レベル」の「バンド図上の位置」と不純物濃度の関係を知る必要があります。

n型Siのフェルミ・レベルEnfのバンド図上の位置（Eiとの差）は、次式で与えられます。

　Enf－Ei = k_BT・ln(Nd/Ni) ・・・（1）

ここで、
Ei：「不純物を全く含まない真性Si」のフェルミ・レベル、
k_B：ボルツマン定数（8.62×10^-5eV/K）、
T ：絶対温度、
Nd：n型Siの不純物濃度（ドナー濃度）、
Ni：真性Siのキャリア密度（1.45×10¹⁰cm^-3）
です。
 

【図1　Siのバンド構造とフェルミ・レベル】

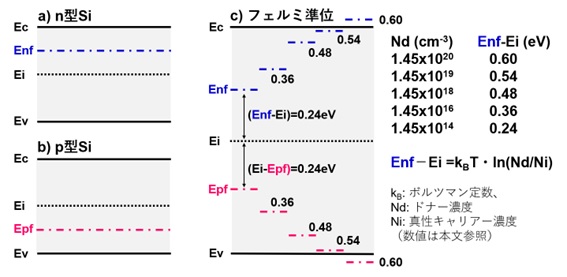
図1は、式（1）を用いて計算した幾つかの結果を示しています。

真性Siのキャリア密度Niが 1.45 x10¹⁰cm^-3 なので、計算を簡単にするために、不純物濃度が異なる5つのn型Si（Nd=1.45×10¹⁴、1.45×10¹⁶、1.45×10¹⁸、1.45×10¹⁹、1.45×10²⁰cm^-3）を想定して、式（1）を用いて、300K（27℃）におけるそれぞれのフェルミ・レベルの位置（Enf－Ei）を計算すると、それぞれ、0.24、0.36、0.48、0.54、0.60eVとなります。

Siのバンドギャップの値は1.12eVなので、その半分は0.56eVです。

従って、最初の三つのフェルミ・レベルの位置はバンド・ギャップの中にあるのに対して、四つ目のSi（Nd=1.45×10¹⁹ cm^-3）のフェルミ・レベルは伝導帯（conduction band）の底（Ec）に非常に近くなり、Nd＝1.45×10²⁰ cm^-3 になると、Enfの位置はEcよりも上になっています。

なお、Nd=4×10¹⁹ cm^-3 のとき（Enf－Ei）＝0.56eV となり、EnfはEcにちょうど重なります。

不純物濃度が非常に高い場合のフェルミ・レベル

Siの原子密度は約5×10²² cm^-3なので、Nd＝1.45×10²⁰ cm^-3 は非常に高い濃度であることがわかります。
Enf≧Ecとなるような高い不純物濃度になると、n型Siは金属のような性質を示すようになります。
n型不純物の濃度がこのように高いとき、「n++型」と表記します。

n++型Siは単なる「特殊な例」ではなく、例えばMOSFETのソース・ドレイン・コンタクト部など、半導体デバイスの色々な部分に使用されています。
（この例については、当連載の次回の記事でご紹介します。）

一方、p型Siのフェルミ・レベルの位置（Epf－Ei）は次式で与えられ、同じ要領で計算できますが、p型Siに関する説明は割愛します。

　|Epf－Ei|=k_BT・ln(Na/Ni) ・・・（2）

ここで、Naはp型Siの不純物濃度（アクセプター濃度）です。

２．pn接合のバンド図（接合直後と平衡状態）

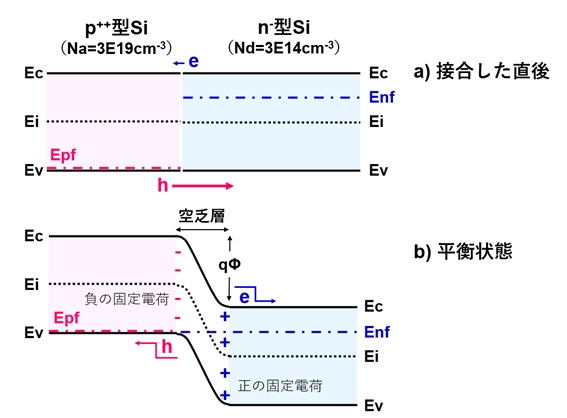
図2に、p++型Si（Na＝3×10¹⁹ cm^-3）と、n-型Si（Nd＝3×10¹⁴ cm^-3）で構成されるpn接合のバンド図（接合直後と平衡状態）を示します。
各領域のフェルミ・レベル（EpfとEnf）の位置については、前節をご参照下さい。

【図2　pn接合のバンド図（接合直後と平衡状態）】

p++型Siとn-型Siが接触すると、n-型Siからp++型Siに向かって電子が拡散し、p++型Siからn-型Siに向かってホールが拡散します。
拡散した電子はp++型Si内のホールと再結合して消滅し、拡散したホールはn-型Si内の電子と再結合して消滅します。

p++型Siの不純物濃度はn-型Siの不純物濃度より５桁も高いので、p++型Siの領域に拡散流入した電子は高濃度のホールと再結合して直ぐに消滅しますが、n-型Siの領域に拡散流入したホールが（低濃度の）電子と再結合して消滅するには、遥かに長い時間がかかります。

このような再結合過程の特徴が、別の記事^*1）で紹介したダイオードやIGBTの「長い逆回復時間」に表れます。電子とホールの拡散現象は、p++型Siとn-型Siのフェルミ・レベルの位置が一致するまで続き、やがて平衡状態に達します。

^*1） 「ダイオードの整流作用と電気特性」参照。

平衡状態におけるバンド図の作成方法

pn接合の平衡状態におけるバンド図を作成する際には、まず初めに、１）p型Siとn型Siのフェルミ・レベルが一致した状態を示す直線を一本引き、次に、２）p型Siとn型Siの「フェルミ・レベルの位置」を考慮しながら、各領域のEc（conduction bandの端）とEv（valence bandの端）を表す線を引き、最後に、３）空乏層領域の線を描きます。

これだけで（半定量的な）バンド図が完成します。この作図手順は、不純物濃度がどのような値であっても同じです。

空乏層の幅

平衡状態では、pn接合界面近傍のn-型Si内には（電子が減った分だけの）正の固定電荷が発生し、pn接合界面近傍のp++型Si内には（ホールが減った分だけの）負の固定電荷が発生するため、これら正負の固定電荷によって発生する電界が生じます。そして、この電界によってホールと電子の拡散が停止し、pn接合界面近傍には（電子とホールが排斥された）「空乏層」が形成されます。

図2に示した例では、n-型Siの不純物濃度はp++型Siよりも５桁も低いため、n-型Si内に拡散したホールが電子と再結合する確率は、p++型Si内に拡散した電子がホールと再結合する確率よりも遥かに低くなり、各領域に形成される空乏層の幅に大きな違いが生じます。

次式（3）で示される「電荷中性の法則」から、p++型Siとn-型Si内に形成される空乏層の幅の違いが類推できます。

　Na・Wp = Nd・Wn　・・・（3）

ここで、WpとWnは、それぞれ、p++型Siとn-型Si内に形成される空乏層の幅です。

拡散電位（電位障壁、エネルギー障壁）

pn接合界面のホールと電子の拡散によって形成される電位障壁は「拡散電位Φ」と呼ばれ、次式で与えられます。

　Φ=(kT/q)・ln（NdNa/Ni²）・・・（4）

ここで、qは電子の電荷（1.60×10^-19C）です。
従って、図2に示した例の場合、拡散電位Φは0.81V（エネルギー障壁は0.81eV）となります。

拡散電位は、逆方向バイアス状態では「電子とホールの移動を阻止する障壁（の一部）」となり、順方向バイアス状態では「電流の立ち上がり電圧」を決定する重要因子となります。
「整流作用」は、この拡散電位の存在によって生じる現象なのです。

空乏層幅の計算

n型Si側に形成される空乏層の幅Wnは次式で与えられます。

　Wn=[(2ε_siε₀NaΦ/[qNd(Nd+Na)]]^1/2　・・・（5）

ここで、ε_siはSiの比誘電率（11.8）、ε₀真空の誘電率（8.85×10^-14 F/cm）です。

図2に示した例ではNaがNdより５桁も大きいので、p++型Si側への空乏層の広がりは無視できます。
従って、式（5）は次式のように簡単化されます。

　Wn=[(2ε_siε₀NaΦ/[qNdNa)]]^1/2=[(2ε_siε₀VdΦ/qNd]]^1/2　・・・（6）

図2に示した例における空乏層の幅Wnは、（Φ=0.81Vなどの数値を式（6）に代入すると）1.87μmとなります（F=C/V：単位の換算に注意）。
つまり、平衡状態における空乏層は、n-型Si側に約2μmも広がっていることになります。

パワー半導体として高い耐圧が必要な場合には数μm程度の空乏層では全く足りないため、n-型Si領域の不純物濃度Ndを遥かに低くしなければなりません^*2）。

^*2） 「パワーMOSFETの空乏層の性質」参照。

３．pn接合のバンド図（逆バイアス状態）

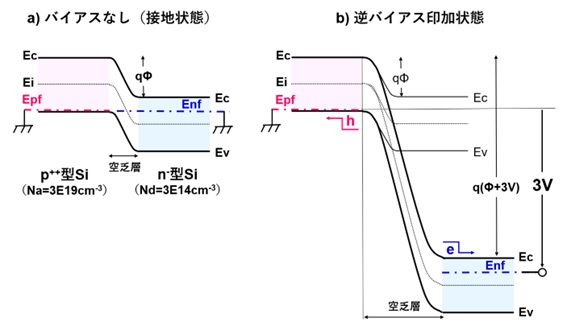
図3に、逆方向バイアスを印加したpn接合のバンド図の例を示します。
p++型Siを接地して、n-型Siに正電圧を印加すると、バンド図は大きく変化します。
（これは、例えば、n型パワーMOSFETの逆バイアス状態と同じです。）

【図3　pn接合のバンド図（逆バイアス状態）】

 
逆方向バイアス（reverse bias）Vrを印加するとΦが（Φ+Vr）となり、空乏層の幅が増加します。
この時の空乏層の幅は、次式で与えられます。

　Wn=[(2ε_siε₀Na(Φ+Vr)/[qNd(Nd+Na)]]^1/2　・・・（7）

逆バイアス状態におけるバンド図の作成方法

Siのバンドギャップは1.12eVですが、手書きでバンド図を描く場合には、バンドギャップを1eVとみなしてしまうと作図しやすくなります。

先ず初めに、１）接地しているp++型Siのフェルミレベルを基準にして、n-型Si領域のフェルミ・レベルの位置を示す線をqVrだけ（図3の例ではVr＝3V）下げた位置に引きます。
次に、２）空乏層のおよその幅を考慮しながら、n型Si領域のEcとEvの線を引き、最後に、３）空乏層の線を引きます。

この手順で、電位障壁の値の変化も矛盾なく描けます。

図3からもわかるように、逆バイアス印加状態では電子もホールも高い接合障壁に遮られるため、反対側に移動することはできません。これが、「整流作用」の一つの重要な特徴（逆バイアス特性）です。

４．pn接合のバンド図（順バイアス状態）

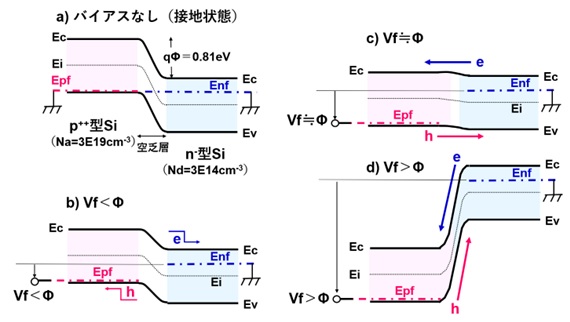
図4に、順方向バイアスを印加したpn接合のバンド図を示します。
n-型Siを接地して、p++型Siに正電圧を印加すると、バンド図は大きく変化します。

【図4　pn接合のバンド図（順バイアス状態）】

 
順方向バイアス（forward bias）Vfを印加した場合、拡散電位Φは（Φ－Vf）となり、Vfの増加と共に減少します。

この例ではΦ＝0.81Vです（図4a）。
従って、順方向バイアスVfの値が0～0.7V程度の時は拡散電位（Φ－Vf）が接合障壁となって電子とホールの移動を阻止するため、このpn接合には電流が流れません（図4b）。

Vfが0.8Vに近づいてくると、伝導帯の電子と価電子帯のホールのエネルギー分布に従って、エネルギーの高いキャリアが障壁を超えて流れ始めます（図4c）。

そして、Vf＞0.8Vになると、（空乏層も消滅して）接合障壁がなくなるため、接合界面を横切って流れる電子とホールの量が指数関数的に増加します（図4d）。これが「整流作用」のもう一つの特徴（順方向特性）です。

要点だけを書き下すとたったこれだけの文章で終わってしまいますが、この解釈には固体電子論やpn接合理論のエッセンスが凝縮されています。
この記事では、電子とホールのエネルギー分布の話や重要な数式の導出過程などは全て割愛しましたので、詳細に関しては専門書をご参照下さい。

５．pn接合の整流作用

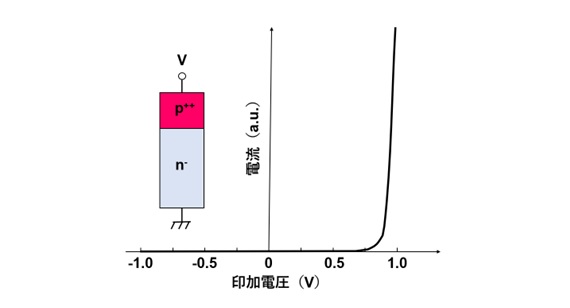
図5に、図3に示したpn接合の電流・電圧特性（整流作用）の模式図を示します。

【図5　pn接合の電流・電圧特性（整流作用）】

順バイアス状態では、上で説明したように、印加電圧Vが0.70V付近までは電流が流れませんが、約0.75V以上になると電流が指数関数的に急増しています。

しかしながら、Vf≒0.8Vまで電流が流れないという特性は、回路特性の観点からは欠点になる場合があるため、実際のデバイス設計においては、不純物濃度の組み合わせやデバイス構造に関する工夫が施されています。

一方、逆バイアス状態でのリーク電流は、図5のようなリニア・プロットの図には表示されないほど小さいため、「電流は流れていない」とみなすこともできます。
ところが、リーク電流をlogスケールで表示すると無視できない大きさになる場合があるため、リーク電流を低減するために、デバイス構造、基板の結晶性、及び製造プロセスに関する研究開発が継続されています。

特に、Siよりもバンドギャップの大きいSiC、GaN、Ga2O3、C（ダイヤモンド）を用いたパワー半導体の研究開発においては、各材料の「Siよりも優れている物性」を最大限に活かすために、リーク電流の発生メカニズムの解明と制御方法の確立が重要課題の一つになっています。
 

次回は、「ショットキー接合」の整流作用に関するバンド図を紹介します。

 
（日本アイアール株式会社　特許調査部　A・Y）

Tweet

Pocket