【機械設計マスターへの道】機械力学の理解に必要な物理学的基礎知識をチェック！
機械力学は、機械の動きと、機械に働く力の大きさや方向などについて調べたり解析したりする学問です。
以前に本連載で、機械力学が扱う現象の中での代表的なテーマであると考えられる「振動」の重要ポイントについて解説しました。
今回は、機械力学を学ぶ上で必要となる物理学的な基礎知識について再確認したいと思います。
目次
１．質点と剛体
機械力学では物体の性質を3つの場合に分けて考えます。
1）質点
物体を、質量を持つが大きさが無い点として扱うことができる場合を質点といいます。
実際にはある大きさを持っていても、回転運動を伴わず直線運動だけを行う場合は、質点として扱うことができます。
2）剛体
物体が、ある大きさと質量を持ち、回転運動を伴い、力を加えても変形は生じない場合を剛体といいます。
回転運動には、加えられた力により物体が転倒するなど向きが変わる場合も含まれ、より現実的な現象を表します。
3）弾性体
力を加えると変形して、力を取り除けば元の形に復旧する物体を弾性体といいます。
弾性体としての定量的取り扱いは複雑になりますので、一般的には物体を質点または剛体として扱い、必要な場合のみ弾性体としての運動解析を行います。
２．質点と剛体の機械力学対比
1）力と力のモーメント
ある剛体の回転軸中心から距離L[m]離れた地点に、F [N]の力を加えるとき M=FL[N-m] を「力のモーメント」といいます。
同じ力を加えたとき回転半径Lが大きいほど、力のモーメントも大きくなります。
棒を使って物を持ち上げる「てこの原理」、あるいはねじ回しで柄の長い方が容易に回せる、ことから理解できます。
シーソーで重い人と軽い人が載って釣り合いをとるときの座る位置を考えることからも理解できます。
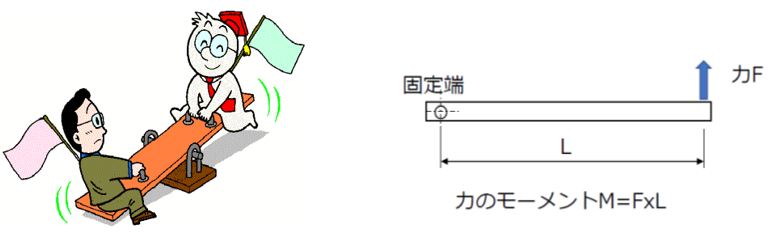
「力のモーメント」は、剛体を回転させようとする回転力のことであり、回転軸を回そうとするモーメント（ねじり）の場合は「トルク」といい、力のモーメントと同じ単位となります。
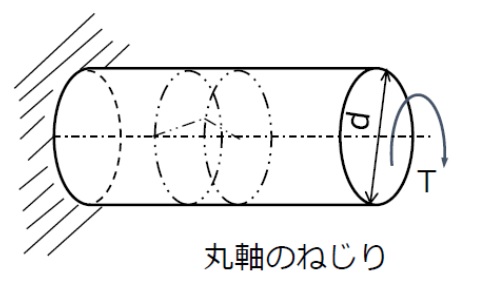
2）質量と慣性モーメント
質点の質量m [kg], 加速度をa [m/s2], 力をF [N]とすれば質点の運動方程式は、F=ma です。
質点の質量に対応する剛体の物理量として、慣性モーメントがあります。
慣性モーメントの記号には通常I を用い、その単位は[kg・m2]となります。
慣性モーメントI は、物体の寸法形状、回転軸位置によって決定されます。
剛体の全質量m[kg]が、回転軸中心からr [m]の位置に集中しているとした場合、
I=mr2 [kg・m2]
質点の運動方程式に対応する剛体の運動方程式は、剛体の回転角速度をα とおけば、次の式で表されます。
M=Iα [kg・m2・s-2]＝[N・m]
３．ニュートンの法則
機械の動きを考えるときに、ニュートンの運動の法則が基礎になります。
1）第1法則（慣性の法則）
物体が、常に現在の運動状態を保とうとする性質のことです。
すなわち、力を受けていないか、力を受けていてもその合力(*)がゼロである場合、動いている物体はその状態を維持したまま等速運動を続けます。
静止している物体は、静止状態を続けます
(*)合力について
力は、その作用する方向を持つベクトル量です。
ある物体(質点、剛体）に大きさが同じで、方向が180°正反対の力が作用しているとき、合力はゼロとなります。
これを力が釣り合った状態といいます。
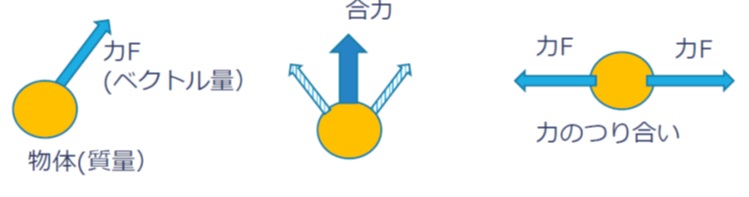
2）第2法則（運動の法則）
物体に力が働くとき、物体には力F と同じ向きの加速度a が生じ、加速度の大きさは力の大きさに比例し、物体の質量m に反比例します。
これを運動方程式で表せば、前述の式 F=ma になります。
力の大きさが同じであれば、質量が大きい（重い）ほど、加速度が小さく、すなわち速度変化率が小さくなります。
質量が小さい(軽い）ほど、加速度が大きく、すなわち速度変化率が大きくなります。
すなわち、同じ大きさの外力に対して、質量が大きいほど動きに変化が生じにくく安定することになります。
このことは振動低減には有利に働きます。
つまり、質量を大きくすることで振動を抑えられる場合があります。
3）第3法則（作用・反作用の法則）
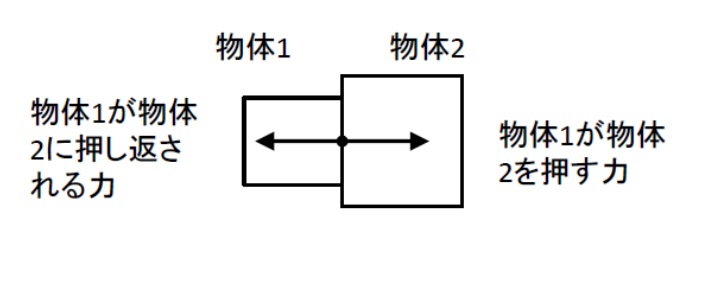
物体1が、物体2に力を作用しているとき、物体1は物体2から反作用の力を受けます。
物体1から物体2に力(作用)を加えると、物体2は物体1へ大きさが同じで逆向きの力（反作用）を同一線上に返します。
このとき作用力と反作用力は、質量には関係なく大きさが等しく、お互いに逆向きとなります。
４．物体の運動
1）直線運動と速度・加速度
物体が直線状に移動するとき、移動した距離と移動に要する時間の比を「速度」といい、単位は [m/s]（SI組立単位）となります。速度を表す記号として、通常はvを用います。
単位時間あたりの速度変化量と、変化に要する時間の比を「加速度」といい、単位は[m/s2](SI組立単位）となります。加速度を表す記号として、通常はaを用います。
加速度は、速度を微分することにより求められます。
すなわち a=dv/dt です。
2）回転運動と角速度・角加速度
回転運動では、直線運動の移動距離に変り、回転角度で考えます。
角度のSI単位は、rad（ラジアン）で、SI組立単位[m・m-1]です。
回転角度と、その角度分の回転に要する時間の比が「角速度」で、通常は記号にω(オメガ）を用い、ω[rad/s]のように表します。
単位時間当たりの角速度変化量と、変化に要する時間の比が、角加速度で通常は記号にα(アルファ）を用い、α[rad/s2]のように表します。
角加速度は、角速度を微分することにより求められます。
すなわち α=dω/dt です。
3）等加速度直線運動の3公式
実際の機械では、発停時あるいは運転中でも加速度が変動することがあり、機械設計では必要に応じて瞬時加速度を求めることがありますが、重力加速度を受けて自由落下する場合のように、等加速度で直線運動する物体の挙動を定量的に表す数式を覚えておくことが基本となります。
物体の初速度をv0、加速度をa（一定）とすれば、t 秒後の速度v は、
v=v0 + at （1） ・・・等加速度直線運動公式①
t 秒間に物体が移動した距離をh [m]とすれば、（1）式を時間で積分することにより、
h=v0t + 1/2at2 (2) ・・・等加速度直線運動公式②
（1）、（2）式より、速度v と移動距離h の間には、次式の関係があります。
v2-v02＝2ah (3) ・・・等加速度直線運動公式③
５．運動量と運動エネルギー
1）力積と運動量
物体に加速度aを与えてt秒後の速度vは、初速度がゼロであるとすれば
等加速度直線運動公式①より、 v=at (1)’
物体の質量をmとすれば、ニュートンの第2法則より、
物体に作用する力Fは、 F=ma (2)
(1)’,(2)式より Ft=mv (3)
(3)式右辺のmvは、力に比例して変化する物体のt秒後の物理量であって、mvを「運動量」といいます。
左辺のFtは、作用する力のt秒間の蓄積であり、Ftを「力積」といいます。
すなわちt秒間に加わる力がF一定であるとき、力積＝運動量 となります。
単位はともに、[N・s ](kg・m・s-1)です。
2）運動量保存の法則
運動量は外から力が加わらない限り保存されます。
物体1と2に外力が加わらず、互いに作用反作用を及ぼしながら速度が変化するとき、一方の運動量の増加と他方の運動量の減少は等しく運動量の総和は一定となります。
すなわち、2つの物体に記号1，2をつけて表せば
m1v1+m2v2=m1v1’+m2v2’
となります。
3）運動エネルギー
質量m [kg]の物体が速度v [m/s]で距離h [m]進んで停止したとします。
この間の加速度a[m/s2]が一定で、初速度がゼロであるとすれば、等加速度直線運動公式③より v2=2ah の関係が成立します。
これを書き換えれば ah=v2/2 (4)
(2),(4)式より 仕事Fh=mah=mv2/2 (5)
(5)式右辺で表される量を運動エネルギーといいます。
4）エネルギー保存の法則
運動エネルギーを記号Ekで表すことにします。
運動エネルギーEkで物体を垂直に上方へ移動し、海抜0[m]からh [m]の地点まで運んで物体が静止したとします。このとき、物体は位置エネルギー（高さ分に相当するエネルギー）を持ちます。
位置エネルギーを記号Epで表すことにすると、
高さh[m]の地点にある物体（質量m [kg]）の持つ位置エネルギーは、
Ep=mgh (g:重力加速度）
Ek=Ep すなわち mv2/2=mgh
移動時に物体が有する運動エネルギーが、位置エネルギーに変換されます。
運動エネルギーと位置エネルギーの総和が一定に保たれることをエネルギー保存の法則といいます。
６．慣性力とダランベールの原理
機械力学は、ある加速度を持って動く物体の挙動を調べる動力学が主体となりますが、加速度を持たないつり合いの状態にある物体を扱う静力学として扱うことで、簡素化できる場合があります。
このとき導入するのが、「慣性力」です。
慣性力の考え方を用いて動力学を静力学に帰結することができることを「ダランベールの原理」といいます。
前出のとおり、物体の質量をm、加速度をaとすれば、ニュートンの第2法則より、物体に作用する力Fは、F=ma です。
この式の、右辺を左辺に移行して(-ma)となる仮想の力を考えると、
F+(-ma)=0
となって、静力学的なつり合いを表す式になります。この-ma のことを慣性力といいます。
たとえば、飛行機が離陸するときシートに押し付けられるように感じるのは、実際に何かの力が体に加わるのではなく、ニュートンの第1法則（慣性の法則）により加速前の状態に留まろうとする体が取り残される結果、-maに相当する慣性力と推進による力maとが釣り合って、体はシート上に静止している、というように理解することができます。
慣性力は円運動にも適用して考えることができます。
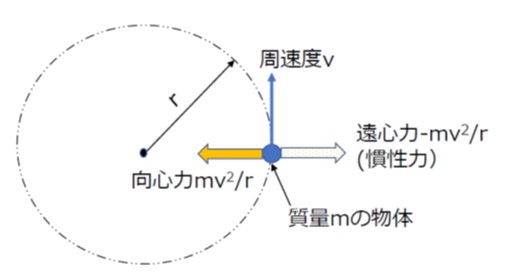
質量mの物体が半径r、角速度ωで等速円運動しているとき、質量の周方向速度はv=rωになります。
このとき回転する物体には、回転中心に向かう加速度 rω2=v2/r と、中心に向かう向心力 F=mv2/r が作用します。
物体は安定した回転状態を維持するので、物体から見れば、向心力と値が同じで反対方向（遠心方向）の力 (-mv2/r) が働いて釣り合っていることになります。
物体(に乗っている観測者)が感じる中心方向反対向きの慣性力(-mv2/r)のことを「遠心力」といいます。
ということで今回は、機械力学を理解するために不可欠と考えられる物理学的基礎知識を挙げてみました。
「機械力学」というと何やら難解な響きがありますが、高校で学ぶ物理を基礎とする延長上にある学問ですので、再確認しておきましょう。
（日本アイアール株式会社 特許調査部 S・Y)
