【電気数学をシンプルに】指数表記と電気部品の性能値

本連載をご覧になっている方は、これから回路設計に取り組まれるという方もいらっしゃるかもしれません。
今回は、電気回路(電子回路)部品を選定する場面などで困らないように、指数表記について解説します。
1.指数表記とは
「指数表記」とは、非常に大きな数や小さな数を表現するための方法です。
例えば、地球から太陽までの平均距離である1[AU](天文単位)は、約1億5千万kmです。
数字でそのまま記述すると、15000000000000000000mです。0が多くて読み書きが大変です。
ここで、指数表記をすると、1.5×1011mとなり、見やすくなります。
このように、指数表記は、m ×Re の形式で表現します。
ここで、mは、指数eによって変化するので仮数と呼ばれています。
Reは、Rをe回かけた値でRの累乗といいます。
ここで、Rを底といい、eを指数といいます。
次のように、指数eが1増えると、10倍することになります。
101=10
102=10×10
103=10×10×10
…
また、指数eは負(マイナス)のときもありますが、103、102、101、100、10-1、10-2…と指数が1減ると、1/10倍することになります。
103=10×10×10
102=10×10
101=10
100=1
10-1=1/101
10-2=1/102
…
2.接頭語
指数表記のRの累乗部分を決められた記号に置き換えることで、さらに読み書きしやすくなります。
日常生活でもよく使われる記号としては、k(キロ)があります。距離を表すときに「家から駅まで2[km]あります。」というように使われるk(キロ)は103を表す記号になります。
このように単位の前につける記号を「接頭語」といいます。
図1に示すよく使われる接頭語については覚えておくと便利です。
接頭語も含め指数表記を用いると、見やすくなるだけではなく、計算の間違いを減らすこともできます。
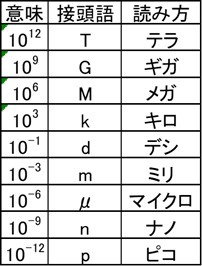
[図1 よく使われる接頭語]
3.チップ抵抗の抵抗値の読み方
指数表記を理解していないと、電気回路部品を選定する場面で困ります。
最も基本的な電気回路部品である抵抗器(抵抗)は、形状によらず見たときに抵抗値がわかるようになっています。
例えば、チップ抵抗の抵抗値は、多くの場合その表面に3桁で表記されています。
この値は、最初の2桁が実数で最後の桁が10の指数を表しています。単位は[Ω]です。
図2のように”683”と表記されていれば、
68×103
=68000[Ω]
=68[kΩ]
になります。
683[Ω]ではありません。

[図2 表面に”683”と表記されたチップ抵抗]
また、3桁で小数点を表すRやLが含まれていることもあります。Lのときは単位が[mΩ]になります。
例えば、
”R33”は0.33[Ω]、
”2L2”は2.2[mΩ]となります。
なお、4桁で表記されているものもあり、その場合は最初の3桁が実数で最後の桁が10の指数を表します。
例. ”1782”は17.8[kΩ]
4. コンデンサの静電容量の読み方
コンデンサの静電容量も抵抗の抵抗値と同様に考えるのですが、単位に注意する必要があります。
コンデンサの静電容量は、4桁で表現されています。
最初の2桁が実数で3桁目が10の指数を表しています。
最後の桁は許容差(アルファベット表記)を表しています。単位は[pF]です。
例えば、”473K”と表記されていれば、
47×103
=47000[pF]
=0.047[μF]
になります。
数値的には47[nF]なのですが、実務上電気回路における単位としては、[pF]または[μF]をよく用います。
【問題】電気回路部品の性能値を正しく読む
では、チップ抵抗値とコンデンサの静電容量の値を正しく読めるか、以下の問題で確認してみましょう。
問1
表面に”100”と表記されたチップ抵抗の抵抗値はいくらか。
《問1の解答》
《問1の解説》
問2
”104J”と表記されたコンデンサの静電容量はいくらか。
《問2の解答》
《問2の解説》
・・・いかがでしたか?正しい読み方を知っていれば簡単ですよね。
ということで今回は、電気回路部品の正しい選定にも役立つ「指数表記」ついて簡単に説明しました。
(日本アイアール株式会社 N・S)














](https://engineer-education.com/wp/wp-content/uploads/2022/08/elearning_AC-circuit1_0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2022/08/elearning_AC-circuit_0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2021/10/electric-circuit-dc0-150x150.png)
































