ポアソン比の基本はこれを読めばOK！

Tweet

Pocket

当連載の前回のコラム「ひずみとは？」では、外力（荷重）を受けて変形する物体の変形度合い（変形率）を表す指標である「ひずみ」について解説しました。

今回は、ひずみに関連して用いられる機械工学用語である「ポアソン比」（Poisson’s ratio）の基本について、出来るだけわかりやすく解説します。
（※前回のコラムで用いた記号を引き続き使用しますので適宜ご参照ください。）

１．ポアソン比とは？

「ポアソン比」（Poisson’s ratio）とは、横ひずみε’の縦ひずみεに対する比率のことをいいます。
ポアソン比はギリシャ文字ν（ニュー）を用いて表します。

前回のコラムでご説明したように、引張荷重に対する横ひずみε’は負（マイナス）、縦ひずみεは正（プラス）となり、圧縮荷重の場合は、正負が逆になります。荷重の種類（引張、圧縮）に関わらず、負（マイナス）記号を付けずに表すため、ポアソン比νは次の式で定義されます。ポアソン比は単位を持たない無次元数です。

　ν = -ε’/ε　　　・・・（1）

２．ポアソン比とポアソン数

ポアソンはフランスの数学者・物理学者Poissonの名前に由来するものです。

（1）式で定義されるポアソン比の逆数を、ポアソン数mといいます。

　m = -ε/ε’　　　・・・（2）

ポアソン数は、Poissonが分子理論を基にして初めて求めた物理量であり、材料によって一定の値となります。
その理論値は4ですが、鉄、銅といった工業用金属材料では、材料ごとに若干相違した値をとり3～4の範囲になるものが多いといわれています。

今日、機械工学ではポアソン数の逆数であるポアソン比を用います。機械材料の場合、荷重方向の変形（縦ひずみ）が機械設計を行う上で第一義的に重要となりますが、材料によって横ひずみがどれくらいの値にあるのかについても知る必要があります。そのため、縦ひずみに対する横ひずみの比率であるポアソン比を使う方が便利といえます。

３．ポアソン比が表す意味

ポアソン比νが大きいということは、例えば引張荷重を受けて縦方向に変形した（伸びた）とき、横方向の変形量（縮み量）もそれなりに大きくなることを示しています。

ゴムのように変形したときの体積変化量が小さい材料の場合には、ポアソン比は大きくなります。（縦に伸びた分、横に縮む）。荷重を受けて変形した時の体積変化量がゼロである場合、ポアソン比は0.5となります。天然ゴムのポアソン比はこれに近い値0.49です。

これに対して金属材料などは、荷重を受けて変形したときの体積変化量が大きいため、縦ひずみに対する横ひずみの割合であるポアソン比は小さくなります（縦に伸びても、横方向にはあまり縮まらない）。

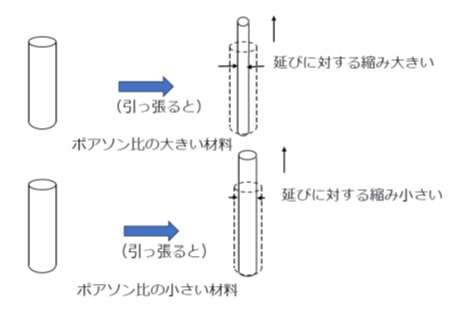
【図1　ポアソン比の大きい材料と小さい材料】

金属材料のポアソン比は？

主な金属材料のポアソン比の値は以下の通りです。

• 鋳鉄： 0.27
• 鋼： 0.28~0.30
• アルミニウム： 0.345
• 銅： 0.343
• 黄銅： 0.35

 
ということで今回は、ひずみに関連する用語である「ポアソン比」について解説しました。
一般的に”ポアソン比が大きい材料は伸び縮みしやすい“といえますが、機械用金属材料の変形のしやすさを表す別の指標（弾性係数）があります。

次回は、応力とひずみの関係を理解するうえで重要となる弾性変形とフックの法則について解説します。
 
（アイアール技術者教育研究所　S・Y）
 

Tweet

Pocket