切削加工の種類と用語、実務者が知っておくべき理論を解説!

目次
1.除去加工の大分類
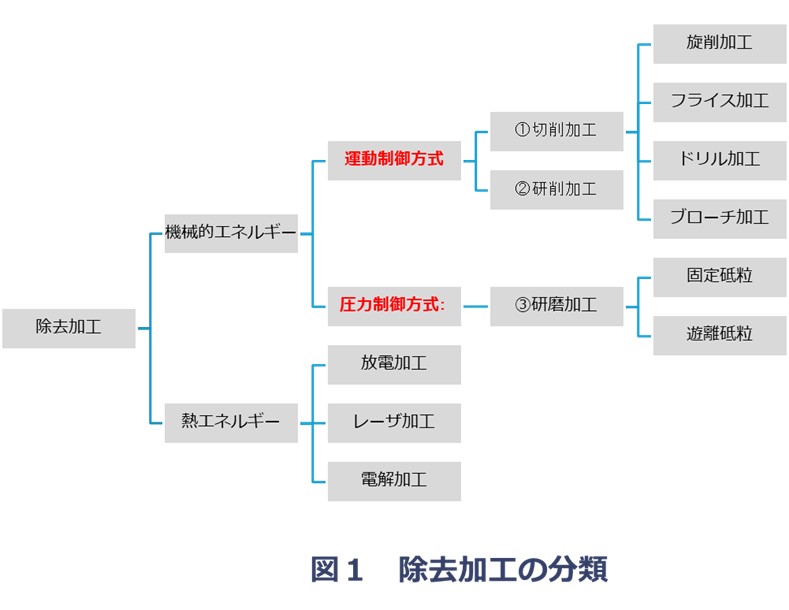
除去加工は、加工に使われるエネルギーの種類により、「回転、圧力などによる機械的エネルギー」と「電気、化学、光等による熱的エネルギー」の2種類に分かれますが、今回は機械的エネルギーによる除去加工について説明します。
この機械的エネルギーによる除去加工も大きく2種類に分類できます。
① 運動制御方式
工具または工作物の回転、直線運動により所要の切り込みを与えて工作物を除去加工するものです。
今回のテーマである切削加工や、研削加工がこれに相当します。
加工精度は、工作物と刃物の相対運動が大きく影響します。
② 圧力制御方式
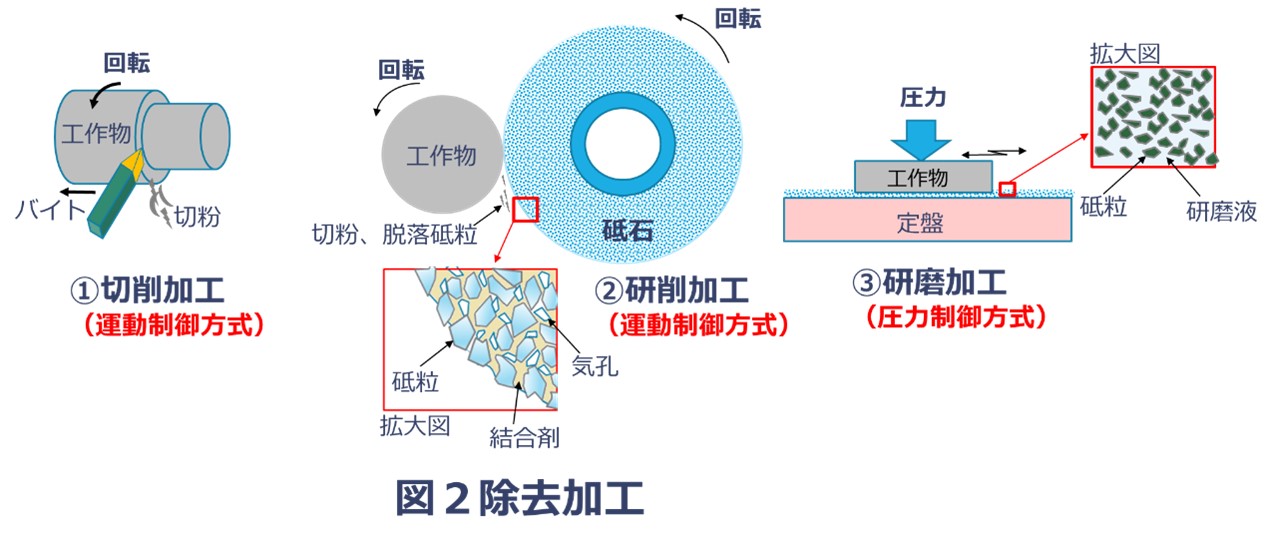
遊離砥粒や固定砥粒を工作物に定圧で押し付けて、金属表面を磨く除去加工法です。
研磨加工がこれに相当します。
加工精度は、圧力により大きく影響します。
一般的には、[切削>研削>研磨]の順に、削り代が小さくなり、加工後の表面粗さが小さくなる傾向があります。
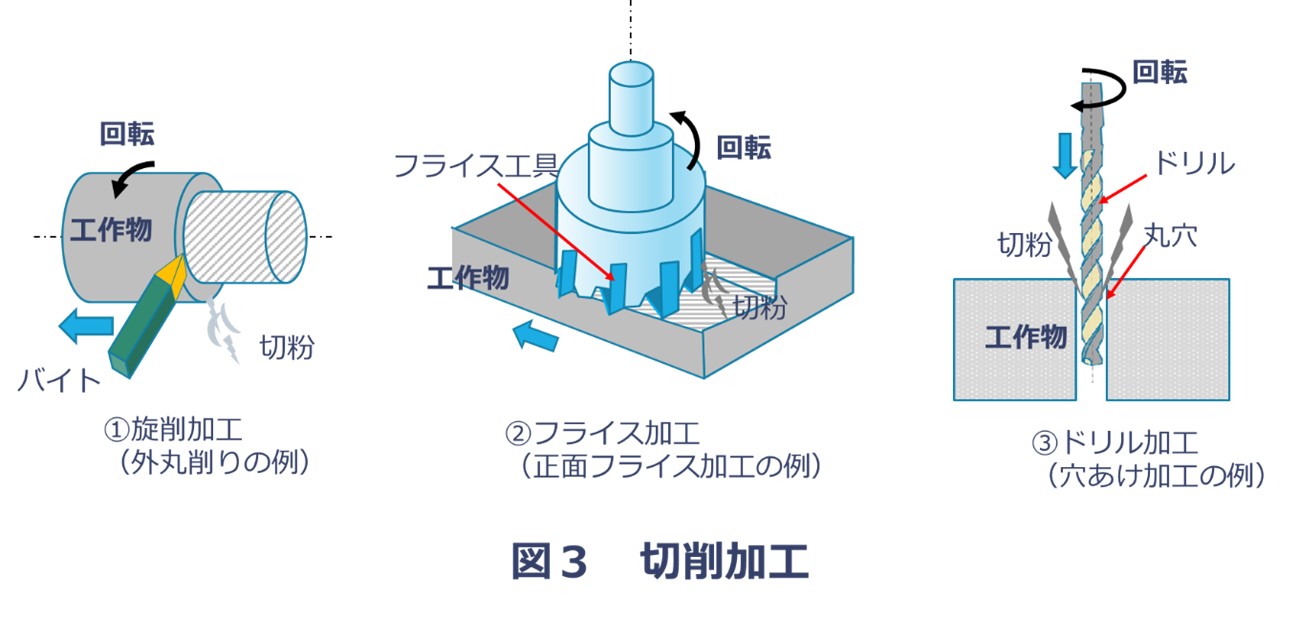
2.切削加工の種類と概要
(1)旋削加工
旋削加工は、工作物が回転する切削加工です。
「旋盤(せんばん)」で工作物を固定し回転させる機械と、工作物を削る「バイト」という工具を使って加工をします。
工作物を回転させて削るため、丸棒(丸形状)が得意な切削です。
刃物は単数(単刃)であるため「単刃(たんぱ)加工」とも呼ばれます。
外丸削り、面削り、テーパ削り、中ぐり、穴あけ、突切り、ねじ切りなどがあります。
(2)フライス加工
フライス加工は、工具が回転する切削加工です。
フライス盤を使って工作物を固定し、工具(フライス工具)を回転させ金属を削る加工です。
フライス加工は四角棒など角材の加工が得意な切削です。
刃物は複数あるため「多刃(たじん)加工」とも呼ばれます。
正面フライス、エンドミル、みぞフライスなど多くの種類があります。
(3)ドリル加工
ドリル加工は、フライス加工と同様に、工具が回転する加工です。
ボール盤を使って工作物を固定し、工具(ドリル)を回転させて、穴あけ加工を行う切削加工です。
ドリル加工も多刃(たじん)加工のひとつで、リーマ仕上げ、ねじ立てなどの加工も行うことができます。
また、その他の切削加工としては、工具または工作物の直線運動による「ブローチ加工」などがあります。
3.2次元切削モデルによる解析と切削の理論
(1)2次元切削モデルとは?
切削加工の中で旋削を例として、工具(バイト)で工作物を削る部分を説明します。
但し、バイトが工作物に対し、直線運動しているとして解析します。
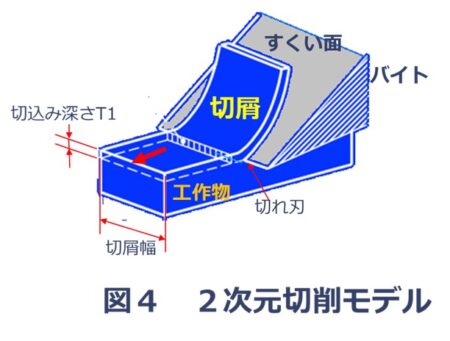
先端の切れ刃に対し、バイトを直角方向に動かしたとき、切屑がすくい面上を横方向に変形せずに、切屑が排出するモデルを「二次元切削」と呼び、図4に示します。
二次元切削モデルは切削現象を理解する上で非常に役立ちます。
なお、参考までに、すくい面上に横方向に変形して切屑が排出する場合は、より複雑な三次元切削モデルになります。
(2)切込み深さT1と切屑厚さT2
金属切削の特徴は、切込み深さT1で削った場合、排出される切屑厚さはT2に変化(塑性変形)していることです。
T2/T1を「切削比」と呼びます。例えば、切削比が3の場合は、排出される切屑の厚さは、切込深さの3倍になり、逆に長さは1/3になります。
このように、切削加工とは、材料を塑性変形させながら削り取る加工であり、切削により排出される金属片のことを「切屑(切りくず)」と呼びます。
バイトにより大きな変形(塑性変形)を与える事から、特にすくい面には高熱が発生します。
(3)すくい角αと逃げ面γ
切屑をすくい取る面を「すくい面」と呼びます。すくい面は切削工具において切削を行う主の面で、この面上を切屑が摩擦しながら通過し、排出されます。
一方、すくい面の反対側にあるのが「逃げ面」です。
すくい面と逃げ面が交わる稜線を「切れ刃」といいます。
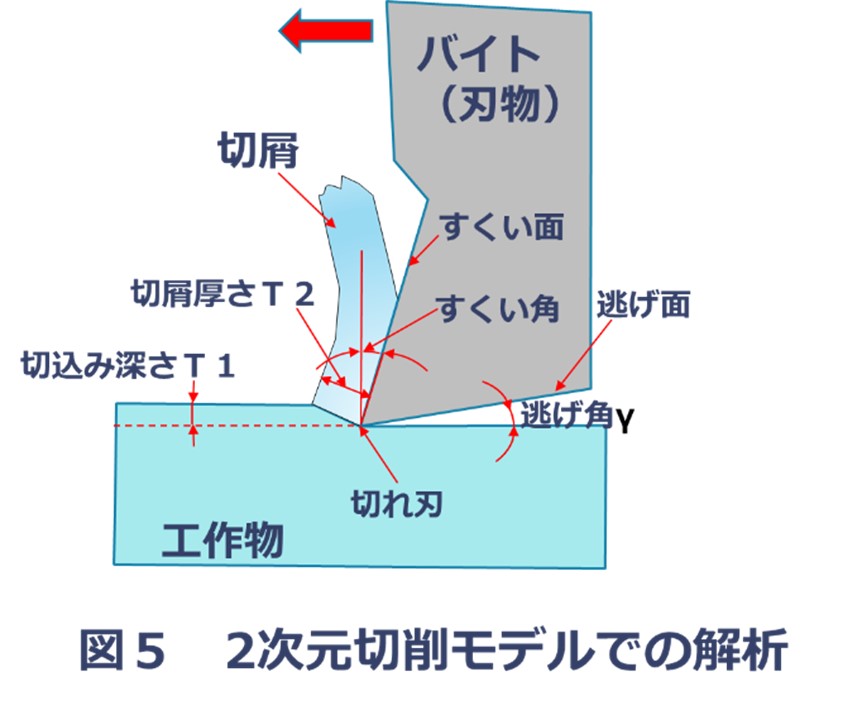
切れ刃の先端で工作物に対し垂線を立てたとき、バイトのすくい面とのなす角αを「すくい角」、また仕上げ面と逃げ面とのなす角γを「逃げ角」と呼びます。
2次元切削工具の刃部は、図5に示すようにすくい面と逃げ面、およびその2面が交わってできる切れ刃によって構成され、その形はすくい角と逃げ角で決定されます。
(4)せん断角φと切れ味の関係
「せん断角」とは、刃物の先端と変形が始まる素材の表面とを結ぶ線と、刃物の進行方向とのなす角のことです。
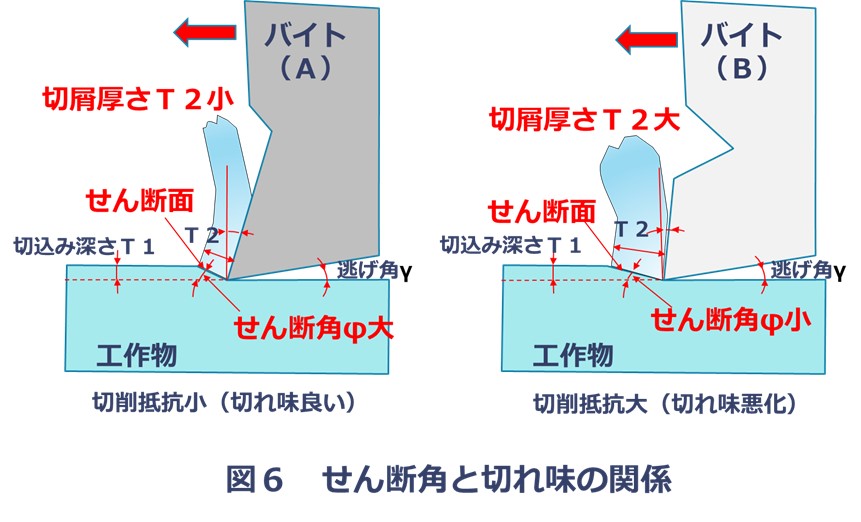
図6は、同じ切込み深さの場合、せん断角の相違により切屑厚さT2がどのように変化するかを示したものです。
せん断角が大きいと、切屑厚さが薄くなっています。つまり、すくい面の切削抵抗が小さくなり、切れ味が良くなります。
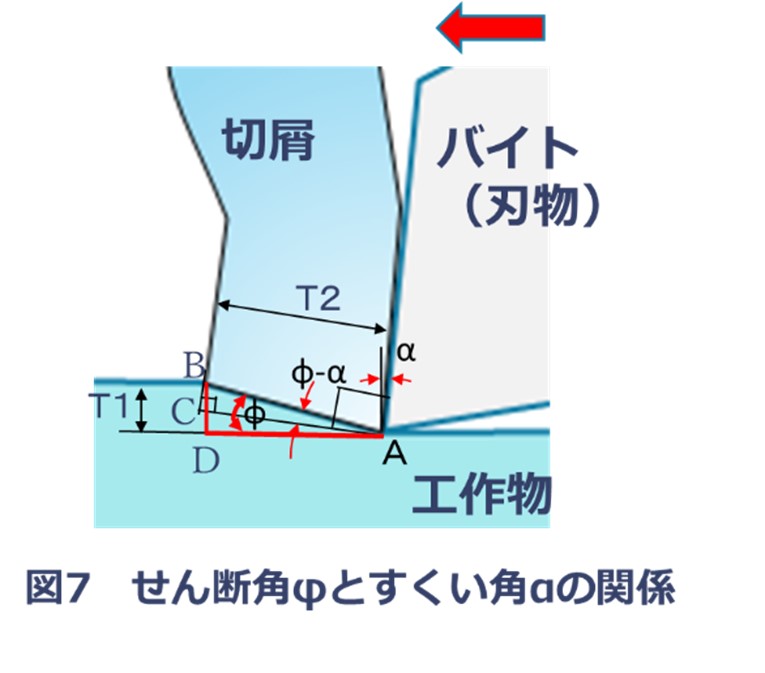
(5)せん断角φとすくい角αの関係
せん断角φとすくい角αの関係は、幾何学的に以下のように求められます。
T1= AB・sinφ(図7より三角形ABD)
T2= AB・cos(φ-α)(図7より三角形ABC)
T1/T2=AB・sinφ/AB・cos(φ-α)= sinφ/cos(φ-α) ・・・式(1)
(AB:せん断面長さ、T1:切込み深さ、T2:切屑厚さ、φ:せん断角、α:すくい角)
三角関数の加法定理に基づき式①を分解し、整理すると
Tanφ=(T1/T2)cosα/[1-(T1/T2)sinα] ・・・式(2)
となります。
以上より、せん断角φは、バイトのすくい角α、切込み深さ設定値T1、切屑厚さ測定地T2 より求められることが分かります。
ところが、この式②からφとαの関係を推定するのは不可能です。このため、実験的にφとα関係を求め解析したものを図8に示します。
図8では「すくい角αが増大すれば,せん断角φも増大する」ことが分かります。
但し、例えばS33Cの切削速度110m/minと170m/minの時の関係を比較すると、切削速度が遅い方がこの関係が強いことも言えます。
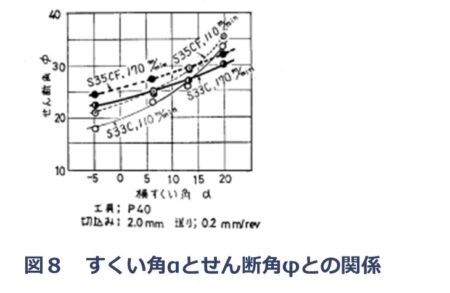
[※出典:「工具の横すくい角が被削性におよぼす影響について」より転載]
3.(4)で述べたように、せん断角が大きいと、切れ味が良くなることから、すくい角が大きい程、切れ味が良くなることがわかり、切削速度も影響していると言えます。
しかし、すくい角を大きくし過ぎると、バイトの刃物が細くなり強度が弱くなるので、バランスのとれた角度を見つけ出すことが重要になります。
以上、今回は「切削加工」の必須知識と重要ポイントをご紹介しました。
次回は「研削加工」の基礎知識を解説します。
(アイアール技術者教育研究所 T・I)
<参考文献>
- 豊島 敏雄, 湊 喜代士 著「工具の横すくい角が被削性におよぼす影響について」福井大学工学部研究報告, 1971年