【品質管理と統計手法】正規分布の基本知識とQCでの活用
目次
1.基本統計量の説明
まず、本コラムで使うデータの特徴を表す「基本統計量」について説明します。
(1)平均値(μ、mean, average)
「平均値」は、最もよく使われている中心を表す統計量の代表値の一つです。
「幾何平均」「調和平均」もありますが、一般的には全データの和をデータ個数で割る「算術平均」が良く知られています。
データから以下の式で与えられます。
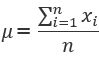
(2)中央値(median)
「中央値」とは、集団のデータを小さいまたは大きい順に並べたときに、中央に位置する値のことです。
データ個数が偶数の場合は中央の2つの数値の平均をとって中央値とします。
(3)最頻値(mode)
「最頻値」は「モード」とも呼ばれ、データの中で最も頻度が高い値です。
(4)分散(σ2)
「分散」はデータの散らばりの度合いを示します。
各データの平均からのずれの 2 乗を合計して、データ数で割ったもので、以下の式によって求められます。
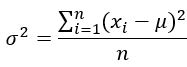
(5)標準偏差(σ)
「標準偏差」は分散の正の平方根です。
分散と同じようにデータのばらつきを表す指標の一つです。
2.正規分布とは?
「正規分布」(Normal distribution)は、確率論や統計学でよく用いられるデータ分布です。
データが平均値付近に集積して、平均値から離れるにしたがって少なくなります。
ドイツの数学者ガウスが正規分布について極めて大きな貢献を与えたことから「ガウス分布」とも呼ばれます。
自然界や人間の行動・性質など様々な現象に対して、よく当てはまります。
例えば:人の身長、体重、血圧、測定の誤差、一定の規格で作ったねじの長さ等が正規分布に従います。
ものづくりにおいても、「製品が基準・規格を満たしているか」などを把握するときに大いに役立ちます。
平均μ、標準偏差σ、分散σ2の正規分布はN(μ、σ2)と表記されます。
3.正規分布の基本性質
正規分布には以下の性質があります。
① 正規分布の形は平均値と標準偏差で決まる
正規分布をグラフで表すと、平均値を中心にして左右に裾野を持つ、釣鐘や富士山のような形をしています。
標準偏差が大きいと、グラフの山は低くなり、裾が広がってなだらかになります。
標準偏差が小さくなると、山は高くなり、とんがった形になります。(図1)
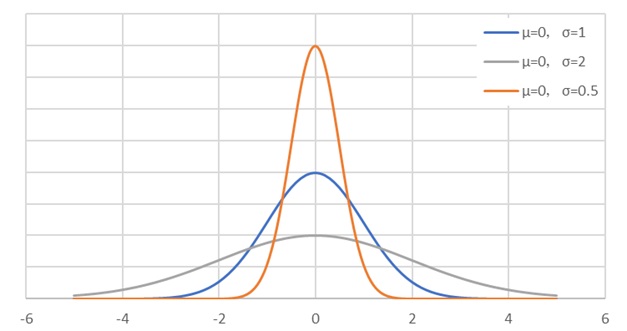
【図1 正規分布グラフの形状】
② 平均値と最頻値と中央値が一致する
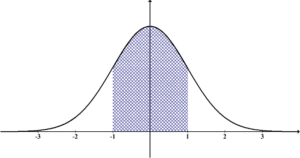
③ 3σでデータを管理できる(図2)
正規分布には以下のことが分かっています。
- μ±1σの間にデータの約68.3%が含まれる
- μ±2σの間にデータの約95.4%が含まれる
- μ±3σの間にデータの約99.7%が含まれる
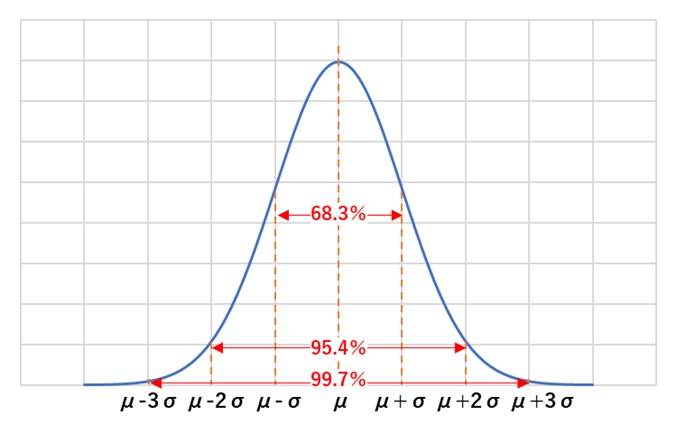
【図2 正規分布の性質】
4.品質管理(QC)での活用
製造現場では、一日あたり数多くの部品が生産されます。
時間やコストの関係で全数検査することは不可能です。
そのため、統計的品質管理手法を用いて、少ない抜き取り数(=サンプル数)で、その母集団の平均やばらつきをより正確に推測する必要があります。
工程が管理状態にあるならば、生産される工業製品の品質特性値の分布はほとんど正規分布に従います。
そのため、このような抜き取り方法(サンプリング)と、ヒストグラム・管理図等の統計的品質管理手法によって測定数値などのデータを分析・管理する場合、正規分布は重要なツールとして活用されます。
正規分布を活用したデータの分析方法は二つあります。
(1)特定数値データの確率を予測する
正規分布からは、任意に設定した製品規格から外れる確率を求めることが可能です。
例えば、加工部品に設定された寸法公差から外れる確率が計算できます。
それにより不良品が発生する確率を統計学的に求められます。
(2)データの管理上限と下限値を決める
一般的に管理上限と下限値が平均値±3σで求められます。
図2に示すように、正規分布では平均値から±3σの範囲にデータの99.7%が含まれています。
言い換えると、0.3%の確率で範囲外となります。
つまり1,000回に3回しか起こらないのです。
もしそのような範囲外のデータが得られたときは、工程で何か異常が発生していると判定できますので、原因の追及と対策の取り組みが必要となります。
(日本アイアール株式会社 特許調査部 Y・X)