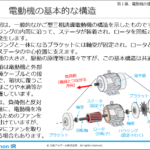
慣性モーメントの基本がわかる！求め方と形状別公式、導出例・計算例まで徹底解説
物体が回転運動をするとき、回転のしやすさ・しにくさ（または回転の止めにくさ）を求める上で重要となる物理量が「慣性モーメント」（イナーシャ）です。英語では”Moment of inertia“といいます。
本記事では、慣性モーメントの意味、公式、導出の考え方、いくつか代表的な形状の物体の慣性モーメント、運動方程式との関係などわかりやすく丁寧に整理して解説します。
目次
１．直線運動と回転運動
（1）質点と剛体
質量を持つが大きさのない点として扱うことのできる物体を「質点」といいます。
質量と大きさを持ち回転運動を行い、力を受けても変形しない物体を「剛体」といいます。
まず、この二つをしっかり押さえましょう。
［※関連記事：ゼロから学ぶ機械力学！絶対に押さえておくべき物理の前提知識をやさしく解説 ］
（2）質点の直線運動と剛体の回転運動
質点の質量m [kg], 加速度をa [m/s2], 力をF [N]とすれば質点の運動方程式は、
F = ma
質点の質量に対応する剛体の物理量が、「慣性モーメント」です。
慣性モーメントの記号にはI を用い、単位は[kg・m²]となります。
慣性モーメントIは、物体の寸法形状、回転軸位置によって決定されます。
なお電流のIと混同をさけるためJを用いることもありますが、本記事においては慣性モーメントをIで表すことにします。
剛体が回転運動をおこなうとき運動方程式は、剛体の回転角加速度をα、トルクをTとおけば、次の式で表されます。
T = Iα [kg・m²・ｓ⁻²] ＝ [N・m]
上記の対比から直線運動の場合は質量が大きいほど動かしにくい（より大きな力を必要とする）のと同様に、回転運動の場合は慣性モーメントが大きいほど回転しにくい（より大きなトルクを必要とする）ことが理解できます。
２．慣性モーメントとは？
（1）質量の位置が回転しやすさ（しにくさ）を決める
慣性モーメントの最も重要な特徴は、「質量そのもの」より “どこに質量があるか（質量分布）” が回転のしやすさ（しにくさ）に強く影響を及ぼすという点です。
物体の総質量が同じであっても、回転軸から遠い場所の質量が多いほど物体は回転させにくくなります。
フィギュアスケート選手のスピンは良い例です。腕を広げると回転が遅くなり、腕を閉じると速くなります。これは腕が外側に広がったことで質量の分布が軸から離れ、慣性モーメントが大きくなるためです。逆に腕を閉じると軸の近くに質量が集まり、慣性モーメントが小さくなって回りやすくなります。
棒を手に持って回す場合でも、真ん中を持つと軽く回せますが、端を持つと急に重く感じます。棒自体の重さは変わらないにもかかわらず“回しにくさ”が変わるのは、回転軸中心に対する質量の位置（分布）が変わることで慣性モーメントが変化するためです。
（2）慣性モーメントの定義式
慣性モーメントを数学的に表すと次のようになります。
ここで、
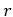：回転軸から各質量要素までの距離
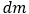：微小な質量要素
物体全体を無数の微小質量要素に分け、回転軸からの距離の2乗をかけたものを積み重ねていくことで、全体としての慣性モーメントが求められます。距離の2乗がかかるため、回転軸から離れた部分に質量が多く分布する形状ほど慣性モーメントは大きくなります。
この定義式はすべての形状に共通する基本ですが、実際には円柱、円盤、球、棒などの形状ごとに計算が行われ、それぞれの公式が導かれます。記事の後半で紹介する公式一覧は、この定義をさまざまな質量分布に適用した結果です。
慣性モーメントは、回転に必要なトルク、回転速度の変化、回転機械を駆動する電動機の選定などと直接関係し、機械設計やロボット工学、車両の運動制御など、多くの分野で必要不可欠な要素となります。
３．慣性モーメントの基本的な求め方
ここでは、前章で述べた慣性モーメントの定義式から各形状物体の慣性モーメントを求める公式を導出する際の、計算の流れや考え方を中心に解説します。
（1）求め方の基本的な考え方
慣性モーメントを計算する際の重要なポイントは、物体の質量分布をどのようにモデル化するかという点です。
物体を無数の微小な質量要素に分割し、それぞれの“軸からの距離”がどれだけ慣性モーメントに寄与するのかを積み重ねて（積分して）いきます。物体の形状の違いにより、微小部分の取り方、座標系の設定、質量密度の扱いが変わるため、積分の形も異なったものになります。
棒、円盤、球を例にとって慣性モーメントの求め方をみていきます。
- 棒： 長さ方向の一次元に質量分布
- 円盤： 半径方向へ広がる二次元に質量分布
- 球： 体積全体に三次元に質量分布
そのため、同じ定義式を使っても、“どの方向に微小体をとるか” が変わるだけで、積分の形は大きく変わり、結果として固有の公式が導かれます。
上記の3種類の形状では、
- 棒：
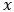を変数にした軸方向の一次元積分 - 円盤： 同心状の微小輪を想定した半径方向の積分
- 球： 球座標系による体積積分
といった計算方法が取られます。
（2）一般的な計算の流れ
公式を導く際の基本手順は、どの形状でもほぼ共通です。
- 回転軸と座標系を設定する
- 微小な長さ・面積・体積の要素を定義する
- その微小部分の質量 dm を物体の密度から求める
- 軸からの距離rを座標の式で表す
- 上記を積分して合計する
このプロセスにより、公式が数学的に導出されます。
（3）実務における“求め方”の位置づけ
実際の設計や計算では、物体の慣性モーメントは通常「既知の公式」を用いて求めます。
しかし、適切に公式を選ぶには、次のポイントを理解しておく必要があります。
- どの軸まわりの慣性モーメントが必要か
- 中心軸なのか偏心軸なのか（平行軸の定理が必要か）
- 中空か中実か
つまり、計算式そのものを覚えるだけではなく、“どのような前提でその公式が成立しているのか” を理解することが重要です。
４．慣性モーメントの導出例
ここでは、前章で述べた基本手順を実際の形状に適用し、慣性モーメントの公式がどのように導かれるのかを具体的に示します。
導出例として扱うのは、機械要素や電動機の回転体などで頻出する 円盤（円板）の中心軸まわりの慣性モーメントです。
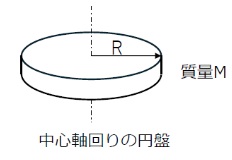
（1）導出の方針：円盤を微小な“輪”の集合として捉える
円盤は「半径方向に質量が広がった二次元形状」です。
円盤を“半径方向に薄い輪（リング）”の集まりとして扱い、半径幅 
の極めて薄い環状部分を 取り出し、その慣性モーメントを積み重ねていく方法を用います。
（2）微小リングの質量 dm を求める
円盤の総質量を
最大半径を
、面密度（単位面積あたりの質量）を
とします。
半径、幅 のリングの面積は
したがって、その部分の質量は
（3）微小リングの慣性モーメント dI を求める
リング状部分のすべての質量要素は、回転軸からの距離がで一定です。
したがって、
これを前式のに代入すると
（4）円盤全体の慣性モーメント I を求める（積分）
半径 0 から 円板外縁部の半径R まで微小リングを積み重ねると円盤全体の慣性モーメントになります。
定積分公式より、
面密度を代入すると、
整理して、下記の通り、円盤の中心軸まわりの慣性モーメント公式が得られます。
５．代表形状の慣性モーメント公式
工学でよく使う形状の慣性モーメントを求める公式は下記のようになります。
（1）断面が一様な棒
- 回転軸が棒の中心にある場合
- 回転軸が棒の端部にある場合
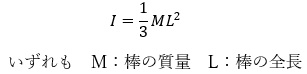
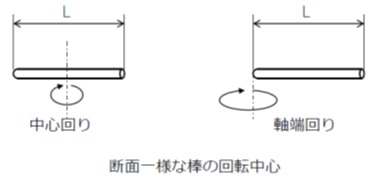
棒の中心に軸がある場合に比較して、端部に軸がある場合には慣性モーメントが4倍の大きさとなります。
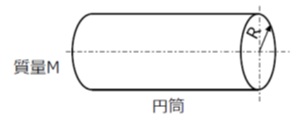
（2）円柱［軸：中心］
中心軸まわりの円柱の慣性モーメントは円板と同じ公式が適用できます。
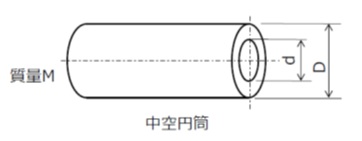
（3）中空円柱［軸：中心］
円柱の質量M, 外径D, 内径dから次式のように求めることができます。
６．慣性モーメントの計算例
円盤を例にとり、公式に数値を代入して計算してみることで、異なる半径に対して慣性モーメントがどのくらい大きくなり、回転しやすさ・しにくさがどの程度変わるのかを数値的に理解しやすくなります。
円盤の慣性モーメント（中心軸まわり）
質量＝2ｋｇ、半径＝0.3ｍの円盤を考えます。
円盤の中心軸まわりの慣性モーメントは次の公式で求められます。
実際に値を代入すると、
この値は、半径が大きくなると半径の2乗に比例して急激に増加します。
半径を0.6 mにすると、質量が同じ場合に慣性モーメントは、半径0.3mの時の値に対して4倍の0.36[kg·m²]になります。
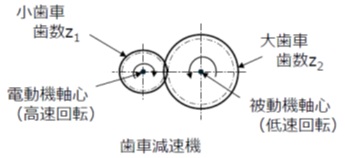
７．減速機を介する場合の慣性モーメント
歯車を介して電動機から被動機に対して減速を行う場合、被動機の慣性モーメントを電動機軸に換算した値は、減速比の2乗に逆比例して小さくなります。
このため電動機の加速に必要なトルクを大幅に削減することができ、電動機からみた負荷（被動機）の慣性モーメントが小さくなるので制御性が向上します。
例えば、電動機側の小歯車の歯数z1と被動機側の大歯車の歯数z2 の比がz1/ z2=0.2、
被動機の慣性モーメントがI=10 [kg·m²]であるとすれば、
電動機軸に換算した被動機の慣性モーメントImは、
Im = I×(z1/ z2)2 = 10×0.04 = 0.4[kg·m²]
となります。
８．慣性モーメントとGD²
SI単位が普及する以前の工学単位系ではGD²（ジーディースクエア）という物理量を用いていました。GD²の単位は[kgf-m²] です。
工学単位系における力の単位は[kgf]であって、値自体はSI単位の質量と同じになります。
Dは直径（半径の2倍）に立脚した数値ですので、慣性モーメントIとGD²の関係は次のようになります。
ただしGD²の単位に[kgf-cm²]が用いられる場合(mではなくcm)もありますので数値換算に注意が必要です。
［※関連記事：機械設計者が知っておくべきSI単位の基礎知識｜換算方法・使い分けなど総まとめ！］
９．設計や解析で慣性モーメントが重要な理由
慣性モーメントは、機械設計、電動機設計、ロボット工学、自動車工学など幅広い分野で活用されています。
《慣性モーメントの用途の例》
- 電動機の負荷計算、起動時間計算
- 車両のヨー慣性モーメントの評価
- ロボットアームの関節トルク計算
- 回転機械の起動・停止特性解析
慣性モーメントがわかると、必要トルク、応答の速さ、などを求めることができます。
おわりに
以上、慣性モーメントとは何かから始まり、求め方、公式、導出の考え方、各形状の一覧、運動方程式との関係、例を使った計算までをまとめて解説しました。
最後に、今回の重要ポイントをおさらいしましょう。
- 慣性モーメントは「回転しにくさ」を表す量
- 単位は kg·m²
- 基本式は
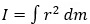
- 形状ごとに求め方・公式が確立されている。
- 回転運動方程式
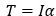
- 円盤、円柱、棒、球などの公式は機械設計で頻繁に利用する
慣性モーメントを理解することで、回転機の設計や解析に役立てることができます。
（日本アイアール株式会社 特許調査部 S・Y)
