一元配置分散分析の具体的な手順をわかりやすく解説！
連載「これならわかる実験計画法」の統計編では、「果物屋さんで売っている桃の中から甘い桃を見分ける方法」という題材を例として、どのような実験を計画し、得られた実験結果をどのように分析すれば合理的な結論が得られるのかを説明しています。
（※題材については、統計編の第1回「《実験計画法と統計》推定と仮説検定の考え方」をご参照ください。）
今回は、統計編の第2回「分散分析の基礎 「ばらつき」の考え方がスッキリわかる！」と、第3回「F検定とは？分散分析による検定の基本を解説」で説明した分散分析を、桃の糖度に影響を及ぼす要因を見つける実験の例に適用して、具体的な手順を説明していきます。
１．要因配置実験と部分配置実験
「要因配置実験」とは、調べたい因子の組み合わせをすべて実験し、主効果と交互作用を検討する方法です。
一つの因子を取り上げる「一元配置実験」、二つの因子を取り上げる「二元配置実験」、さらに三つ以上の因子を取り上げる「多元配置実験」もあります。
［※要因配置実験の基礎知識は《実験の手順》要因配置実験と直交配列表実験のポイントもご参照ください。］
一方、調べたい因子の組み合わせのすべてではなく、一部の組み合わせのみで実験を行う場合もあり、「部分配置実験」と呼ばれます。部分配置実験では、交互作用のすべては検討できませんが、直交配列表を利用して取り上げるべき交互作用を限定することで、実験回数を抑えることができます。
このコラムで紹介している実験では、桃のサイズと色に注目し、すべての組み合わせで糖度のデータを取りましたので、二元配置実験と言うことになります。この実験結果を使って、一元配置実験、二次元配置実験での分散分析の手順を見ていきます。
２．一元配置分散分析の手順
色については無視して、実験結果を、サイズが糖度に及ぼす影響を見るための一元配置実験で得られたデータとして扱います。第3回のコラムで説明した分散分析の基本的な手順に則って、進めていきます。
- ① 帰無仮説の設定
「桃のサイズと糖度は相関していない」とします。 - ② 有意水準の設定
「めったに起きない」の基準を５％に設定します。 - ③ 統計量の算出
以下の通り進めます。
表1は、桃の糖度の実験の全データですが、色については無視して、表2のように、1因子（サイズ）、3水準（大・中・小）の一元配置実験として分散分析で調べます。
各水準に４個、計１２個のデータがあります。
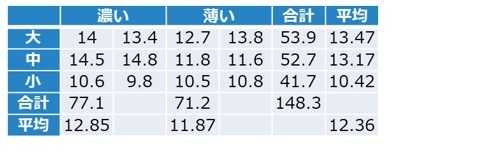
【表1 桃の色とサイズ毎の糖度のデータ】
【表2 色について無視した桃のサイズ毎の糖度のデータ】
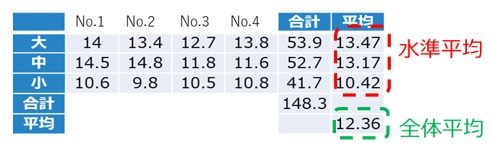
先ず、全体のばらつきを要因効果と誤差によるばらつきに分解します。
得られた偏差から、平方和を計算します。
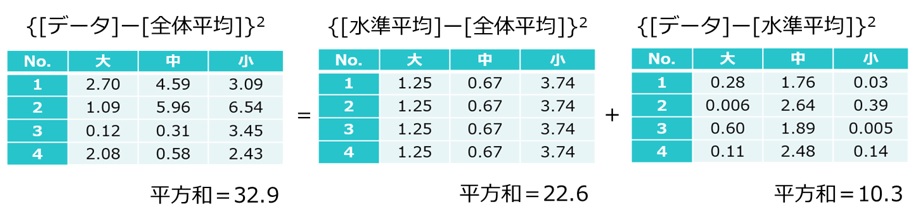
このように全体の平方和（32.9）を、要因効果による平方和（22.6）と誤差による平方和（10.3）に分解することができます。要因効果による平方和と誤差による平方和を足したものが、全体の平方和になっていることを確認してください。
全体のばらつきを要因効果と誤差によるばらつきに分解したとき、要因効果による平方和と誤差による平方和を足したものが、全体の平方和になることは数式を展開していけば証明できますが、煩雑になりますのでここでは省略します。
得られた結果を表3のようにまとめます。
【表3 分散分析表】
この実験では、要因Aは桃のサイズで、水準数は３（大、中、小）です。全データ数は12ですから、全自由度は11です。
これらの数字と、上の計算で得られた平方和を表に入れていくと、表4のような結果が得られます。
【表4 分散分析表】
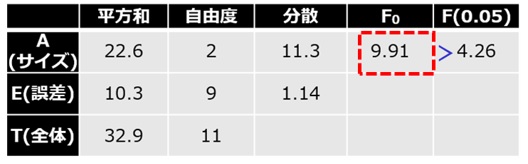
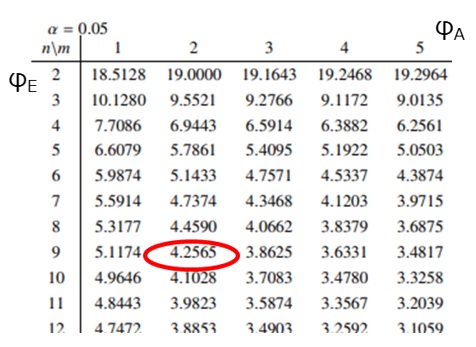
ここで得られたF0（=9.91）を、自由度φA（=2）、φE（=9）のF分布表（表5）で得られるF(0.05)の数字（=4.2565）と比較すると、F0＞F(0.05, φA, φE)であるため、有意水準5%で帰無仮説は棄て、有意水準5%で桃のサイズにより糖度に違いがあると判定されます。
【表5 自由度φA、φEのF分布表（抜粋）】
しばらく数字を追いかけてきましたが、ここで仮説検定でやろうとしたことの確認をしておきましょう。
仮説はあくまでも母集団の性質について設定します。
母集団の桃のサイズによって、糖度に差はないという仮説を立てました。もしそうだとしたら、大中小のサイズごとに4個、計12個の標本を母集団から取って糖度のばらつきを調べたときに、サイズ水準間の糖度の分散が、サイズ水準内の糖度の分散より9.91倍も大きいなどということはめったに起こらないはずである。
従って、母集団の桃の糖度はサイズによって異なっているに違いない。
ただし、5％危険で判定していますので、本当は母集団の桃のサイズと糖度に相関がなかったとしても、大中小のサイズごとに4個、計12個の標本を取って糖度のばらつきを調べることを100回繰り返したとしたら、そのうち５回はサイズと糖度に相関があるという誤った結論を導いてしまう可能性があり、今回の標本がまさにそのケースだった可能性があることも認識しておく必要があります。
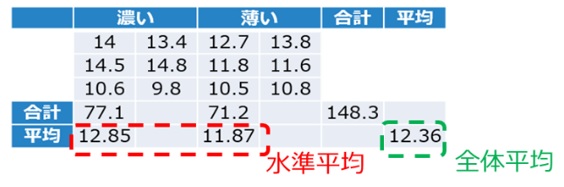
今度は桃の色によって糖度に違いがあるかについて、サイズは無視して、 1因子（色）、２水準（濃い・薄い）の一元配置分散分析で検討してみましょう。各水準に６個、計１２個のデータがあります。
【表6 サイズについて無視した桃の色毎の糖度のデータ】
手順はサイズについて検討した時と同様です。
- ① 帰無仮説の設定
「桃の色と糖度は相関していない」とします。 - ② 有意水準の設定
「めったに起きない」の基準を５％に設定します。 - ③ 統計量の算出
全体のばらつきを要因効果（桃の色）と誤差によるばらつきに分解し、それぞれの平方和を求めます。ここでは詳細は省きますが、時間がある方は計算してみて下さい。
結果として分散分析表は、表7のようになります。
【表7 分散分析表】
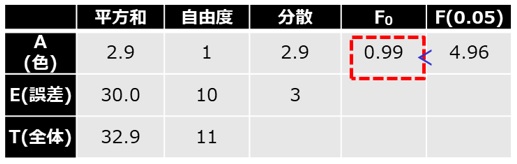
ここで得られたF0（=0.99）を、自由度φA（=1）、φE（=10）のF分布表（表5）で得られるF(0.05)の数字（=4.9646）と比較すると、F0＜F(0.05, φA, φE)であるため、有意水準5%で帰無仮説は棄てられず、有意水準5%で桃の色により糖度に違いがあるとは言えません。
ここで、「桃の色により糖度に違いがない」とは言っていないことには注意が必要です。単に証拠が不十分であったというだけで、色によって糖度が違うのか違わないのか、結論は出ていない状態です。
また、注目している因子以外の原因によるばらつきは、すべて誤差とみなしていることに注意して下さい。より具体的に言えば、サイズによる糖度の違いを誤差とみなす、色に注目した分析では、サイズによって糖度が違うことの影響が大きいため、色の影響が見えにくくなっている可能性があります。
サイズに注目した分散分析では、色の影響を無視（誤差として扱った）しましたが、それでもサイズと糖度に相関がないと仮定するとめったには起こらないようなことが起こっていると言えたということは、それほどサイズの影響が大きいということだと解釈できます。
ここまで来ると、考慮しなければならないのが、次回説明する交互作用です。
（日本アイアール株式会社 H・N)
