F検定とは?分散分析による検定の基本を解説

連載コラム「これならわかる実験計画法」の統計編では、「果物屋さんで売っている桃の中から甘い桃を見分ける方法」を題材に、どのような実験を計画し、得られた実験結果をどのように分析すれば合理的な結論が得られるのかを説明しています。
(※題材については、統計編の第1回「《実験計画法と統計》推定と仮説検定の考え方」をご参照ください。)
今回は、統計編の第2回で解説した「ばらつき」の考え方(分散分析の前提)の続きとして、分散分析の概要と検定の流れをご説明します。
1.F検定とは?
実験で得られる特性について、ある因子に注目した時の分散と、誤差の分散との比をとって、それがある値よりも大きければ「ばらつきと因子に相関がない」とは言えないのではないか、とういうことを明らかにする検定を「F検定」といいます。
桃の例で言えば、特性は糖度で、ある因子とは桃のサイズです。
F検定では、分散の比を利用した値(F値)として、図1のようなF分布曲線を使います。
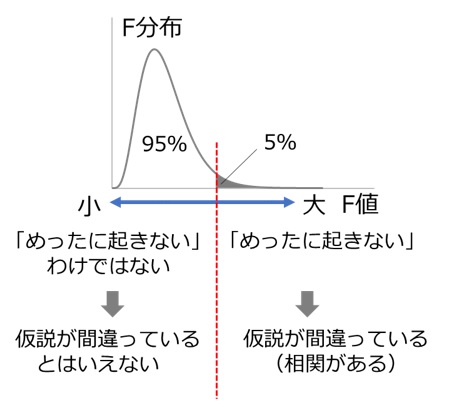
【図1 F分布曲線】
桃の例のF検定では、「サイズと糖度は相関していない」(帰無仮説)と仮定したうえで、サイズに注目した時の分散と誤差の分散との比が右側5%に含まれるという結果を得た場合、「めったに起きない」と判断し、「サイズと糖度は相関していない」という帰無仮説は棄てられます。
2.分散分析による検定の手順
「桃のサイズと糖度の関係」を例に、分散分析による検定を行う場合の基本的な手順を説明します。
(1)帰無仮説の設定
「桃のサイズと糖度は相関していない」と設定します。
(2)有意水準の設定
「めったに起きない」の基準を設定します。
5%(もしくは1%)とします。
(3)統計量の算出(分散VA:要因の効果、分散VE:誤差)

算出結果を表1のような分散分析表にまとめます。
【表1 分散分析表】

(4)判定
F0=VA/VE≥F(0.05,φA,φE)の時、
有意となり、帰無仮説は棄てる
⇒サイズにより糖度に差がある
⇒桃のサイズと糖度に相関がある と判断します。
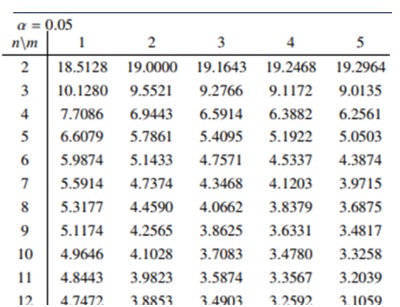
F(0.05,φA,φE)は自由度がφAとφEであるF分布曲線の上側確率5%点で、表2のようなF分布表から求められます。
【表2 自由度φA、φEのF分布表(抜粋)】
分散分析では、例えば3つの群でデータを得た場合、3つの平均値のいずれかに差があることはわかりますが、どの群の間に差があるかについてまでは判断できません。
どの組み合わせで差があるかさらに調べるためには、多重比較という方法もありますが、入門の域を超えているので省略します。
次回の「一元配置分散分析の具体的な手順をわかりやすく解説!」では、この連載コラムで例として使ってきた、桃のサイズ、色が糖度に与える影響を調べる実験について、分散分析を適用する手順を追っていきます。
(日本アイアール株式会社 H・N)













](https://engineer-education.com/wp/wp-content/uploads/2022/09/experimental-design_statistics_1-150x150.png)
![英語版「実験計画法入門[統計編]」/Introduction to Design of Experiments Method – Statistics Edition(eラーニング)](https://engineer-education.com/wp/wp-content/uploads/2023/09/img-design-experiments-method_english-150x150.png)