【早わかり電子回路】カウンタ回路とは?前提となる2進数の理解から丁寧に解説

デジタル回路のうち、数を数える回路を「カウンタ回路」と呼びます。
「カウンタ」とは、数を数える(カウントする)装置を指しますが、デジタル回路の場合は、回路にパルスが入力されたときにパルスの数を数える論理回路になります。
1.2進数と10進数
デジタル回路は、オンとオフ、すなわち、1と0で表されます。
この、1と0を扱うのは、2進数が使われています。2進数は数を表現するときの表現方法の1つです。
普段我々は、10進数を使用していますが、他には、2進数や16進数など様々な数の表現方法があります。
「10進数」というのは、0から1つずつ数を足して行き、9に1を足した瞬間に「桁上がり」が発生することで初めて2桁の数である10になります。
その後も各桁が9の次の数になる毎に桁上がりが発生するのが10進数のルールです。
10進数では9の次の数で桁上がりが発生するので全ての数を0~9の数字だけで表現することができます。
これに対して「2進数」というのは、0から1つずつ数を足して行くときに、1に1を足した瞬間に「桁上がり」が発生するルールです。
各桁が1の次の数、すなわち2になる毎に桁上がりが発生するのが2進数という数の表現方法になります。
スタートの数が0ですが、0の次の数は1です。1の次はもう桁上がりが発生してしまうので、10となります。
その次は、11です。11の次はまた1桁目で桁上がりが発生して、繰り上がった2桁目でも桁上がりが発生するので、100になります。
2進数の数の増え方を見てみましょう。
2進数では、[0 → 1 → 10 → 11 → 100 → 101 → 110 → 111 → 1000 ・・・]となります。
2進数と10進数の対応表は、下の図1のようになります。

【図1 2進数と10進数の対応表】
2進数では全ての数を0と1の2種類の数字だけで表現することができます。
0と1だけで全ての数を表現できるという特徴は、全ての情報をONとOFFの組合せだけで表現するコンピュータの動作とは相性が良いのです。
このような理由で、コンピュータ内での数の表現は2進数に合わせて作られています。
2.カウンタ回路とフリップフロップ
カウンタの回路は、フリップフロップ回路を用いて実現できます。
ここでは、T型フリップフロップ(T-FF)を用いて考えてみましょう。
「T型フリップフロップ」は、入力パルスが入るたびに出力が反転するフリップフロップです。
- フリップフロップの基礎知識はこちらをご参照ください。
では、図2でカウンタ回路に用いるT-FFの例を見てみましょう。
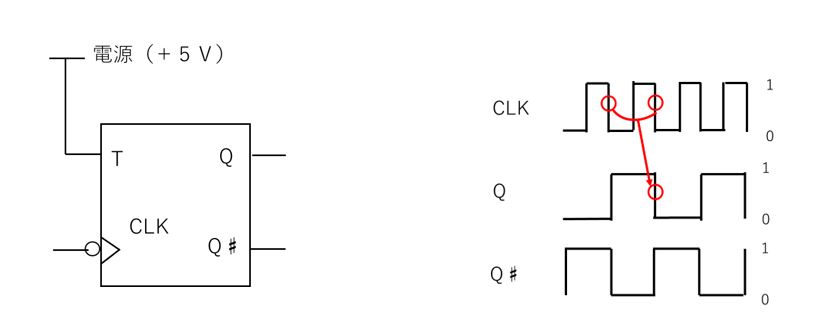
【図2 T型フリップフロップ(カウンタ回路)】
図2はT-FFの入力端子を電源に接続し、ハイレベルに固定したもので、CLKパルスが2個入力されるたびにQとQ♯に1個のパルスが出力される様子を示しています。(赤で示した部分)
T-FFを直列に接続した回路
図3はT-FFを3個直列に接続した場合の回路構成で、図4はそのタイムチャートです。
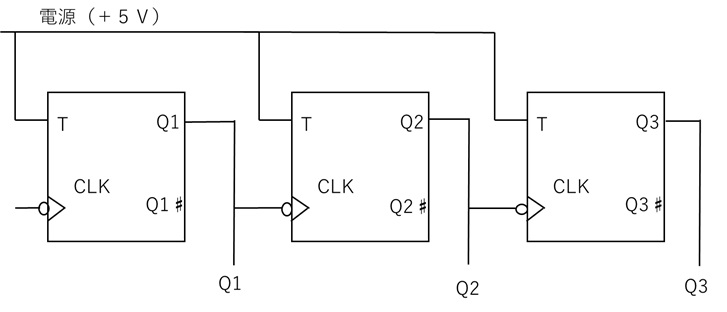
【図3 T型フリップフロップの直列構成】
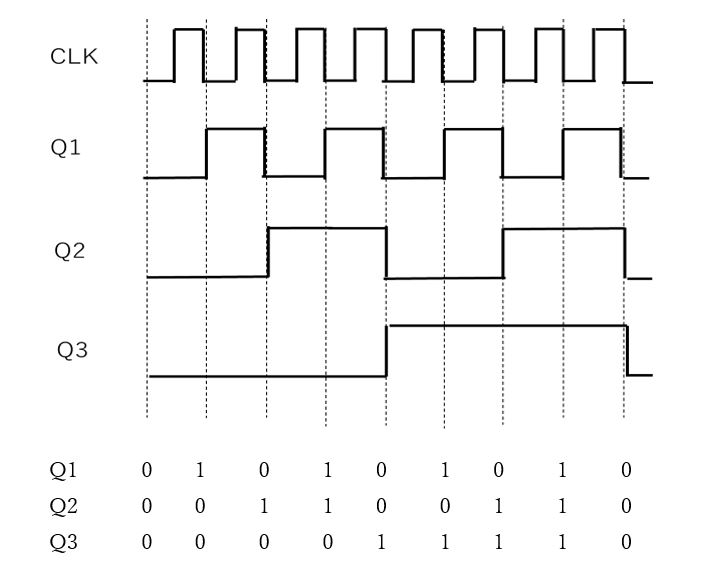
【図4 タイムチャート】
図3ではT-FFを3個直列に接続しており、図4のように、T-FF1段ごとに2個のパルスが1個のパルスに変換されています。そして、出力Q1、Q2、Q3を2進数の1桁目、2桁目、3桁目に対応させると、(Q3、Q2、Q1)が(0、0、0)から、(0、0、1)・・(1、1、1)に対応していて、2進数の000から111までカウントしていることになります。
そして、図1の表と対応させると、10進数の0から7まで数えていることになります。
この回路では、出力111の次は000に戻りますが、接続するT-FFの数を増やしていけば、数えられる範囲を広くできます。
n個のT-FFを接続すれば、0から「2のn乗」-1個 の2進数がカウントできることになります。対応する10進数も数えることができます。
カウンタ回路は身近な電子機器・装置で使われています
ということで、今回はカウンタ回路について説明しました。

カウンタ回路は、様々なところで使用されており、身近なところでは、デジタル時計があります。時計は、1秒(1Hz)のパルスを60回数えて1分、3600回数えて1時間、というようにカウントして表示している装置ということになります。他にも、デジタル回路を使った装置には、ほとんど使用されているといってもよいでしょう。
[※関連コラム:カウンタICの仕組み(バイナリカウンタの例で解説)はこちら]
(日本アイアール株式会社 特許調査部 E・N)














](https://engineer-education.com/wp/wp-content/uploads/2021/10/electric-circuit-dc0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2021/10/Circuit-element0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2022/08/elearning_AC-circuit1_0-150x150.png)































