【早わかり電子回路】デジタル回路のコンパレータを解説
デジタル回路は、論理回路とも呼ばれていますが、論理回路のうち入力信号の組み合わせだけで出力が決まるような論理回路を「組み合わせ回路」と呼びます。（※組み合わせ回路の解説ページはこちら）
「組み合わせ回路」のうち今回は、コンパレータについて説明します。
１．コンパレータとは？
「コンパレータ」とは、2種類のデータの大小関係を調べる回路のことで「比較器」とも呼ばれます。
２種類のデータを比較すると、一致するときと、一致しない時（不一致）があります。また、どちらが大きいかを調べることもできます。
２．一致回路、不一致回路 （コンパレータ）
「一致回路」は、二つの入力が一致しているときに“１”を出力します。
「不一致回路」は、二つの入力が一致していないときに“１”を出力します。
まず、図1に一致回路の真理値表を示します。
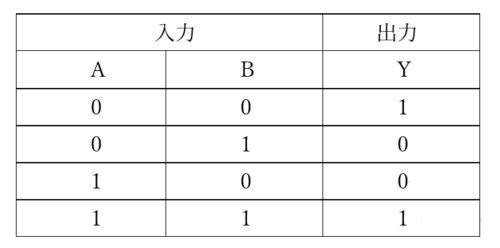
【図1 一致回路の真理値表】
図1の真理値表では、入力AとBが同じとき（一致）、出力Yは１になり、AとBが異なるときは、出力Yは０になっています。
次に、図2に不一致回路の真理値表を示します。
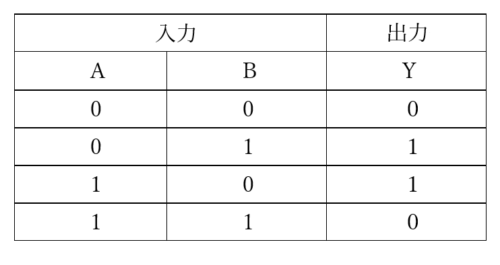
【図2 不一致回路の真理値表】
図2の真理値表では、図1と反対で、入力AとBが同じとき、出力Yは０になり、AとBが異なるときに（不一致）、出力Yは１になっています。
真理値表の論理を見ると、図2は、排他的論理和になっていることがわかります。
また、図1は、逆の排他的否定論理和になります。
図3に図1の回路図、図4に図2の回路図を示します。
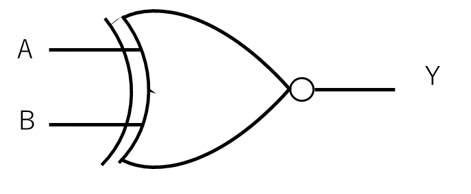
【図3 一致回路の真理値表の回路図】
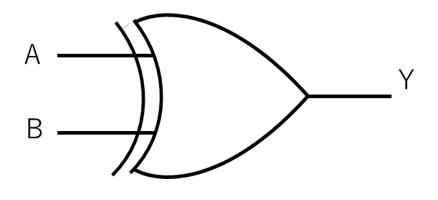
【図4 不一致回路の真理値表の回路図】
４．多数決回路
「多数決回路」は、例えば、3つの入力があるときに、そのうちの2つ以上が“１”になる場合の出力を“１”とする回路です。
図5は、3入力多数決回路の真理値表です。
図5は、3つの入力をそれぞれA、Ｂ、Cとし、出力をYとした場合に、3入力の内、入力の2つ以上が“１”になった場合のみ、出力Yが“１”となる真理値表となります。
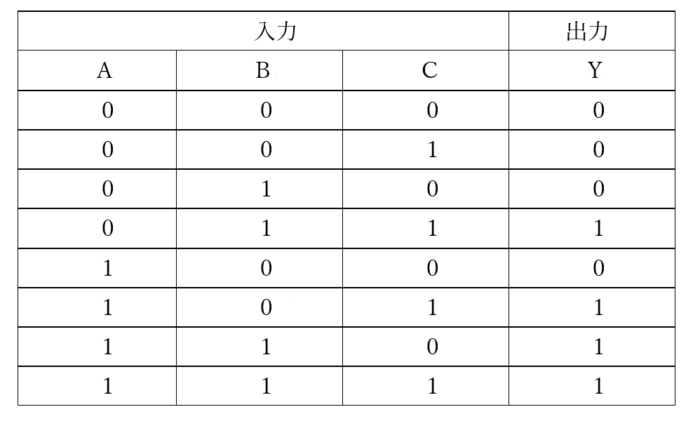
【図5 ３入力多数決回路の真理値表】
図5の真理値表を回路図にしたものが、図6になります。2入力の“１”がAND回路で選択されて、OR回路を通る形になっています。
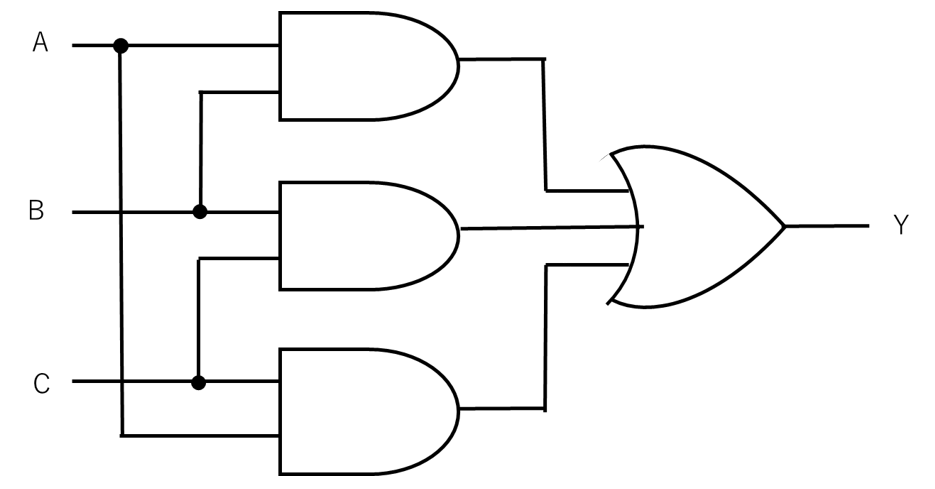
【図6 ３入力多数決回路の真理値表の回路図】
多数決回路は、高信頼化のための冗長設計においてよく用いられています。
３．大小比較回路
一致、不一致回路では、2つの入力の一致か不一致かはわかりますが、入力の大小関係はわかりませんでした。
「大小比較回路」はこの大小関係を見るもので、2つの入力のうち決められた方の値が大きいときに“１”を出力します。図7にその真理値表を示します。
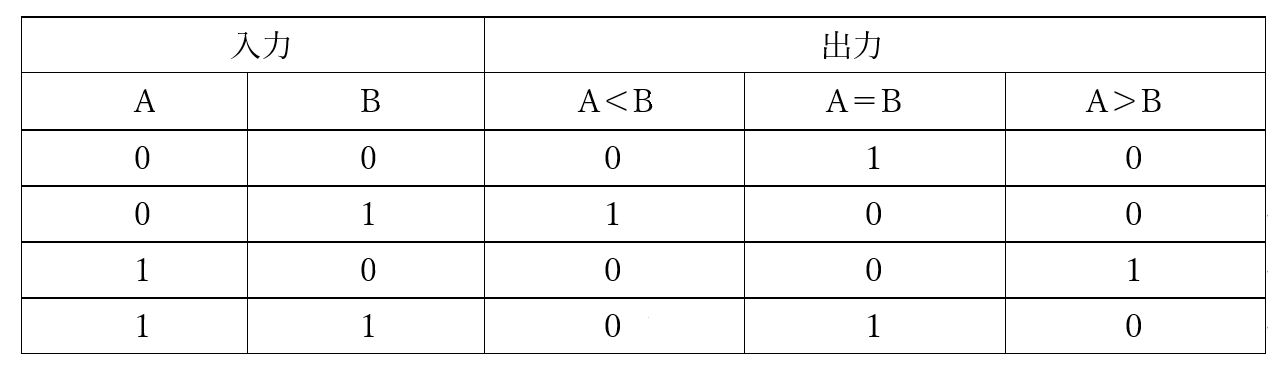
【図7 大小比較回路の真理値表】
図7では、AとBを比較して、３つの大小関係に分けています。
図7を回路図にしたものが図8になります。
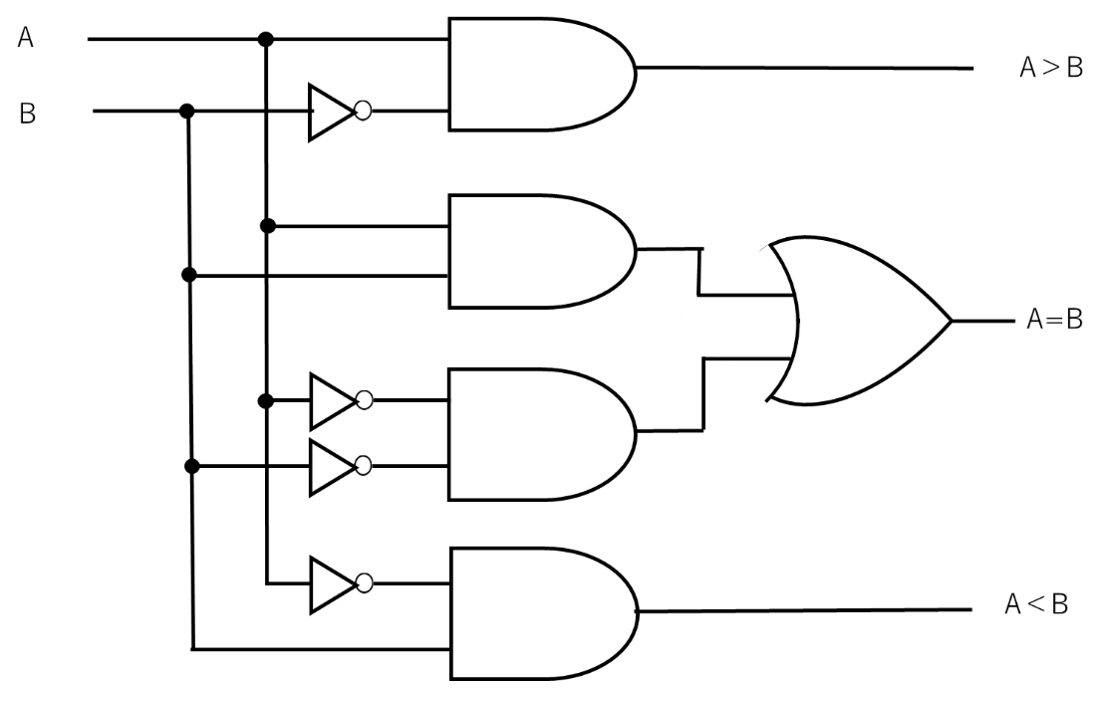
【図8 大小比較回路の真理値表の回路図】
図8では、AとBの各場合に対応したAND回路を設けて処理しています。
５．パリティチェック
「パリティチェック」は、データの誤り検出方式の一つで、ビット列中に含まれる“１”の数が偶数か奇数かを表す符号を算出してデータに付加する方法です。
最も単純な誤り訂正符号で、1ビットの誤り検出しかできませんが、算出や検証が容易で高速なため、よく使われています。
データはコンピュータ上では“０”と“１”が並んだビット列として表されていますが、これを一定の長さのブロックごとに区切り、各ビットの値を足し合わせた値が奇数であるか偶数であるか（“１”の数が奇数か偶数か）を表す1ビットの値（パリティビット）を末尾に付加します。
パリティを含むデータを受け取った側は、各ブロックごとに同じようにパリティを算出し、付加されたものと比較します。
両者が一致すれば、そのブロックには誤りが存在しないか偶数個あることが分かり、一致しなければ奇数個の誤りがあることが分かります。
たまたま送信側と受信側のデータの“１”の数が同じになってしまった場合などには誤りを検出できませんが、簡単なので使われることが多いです。
このパリティを算出する回路も比較器（コンパレータ）の応用といえるでしょう。
パリティチェックの回路図と誤り検出の考え方
上記で、「ビット列中に含まれる“１”の数が偶数か奇数かを表す符号を算出して」とありますが、“１”の数をわざわざ数えなくても、デジタル回路では、“１”と“０”しかないので、図9のような回路で示すことができます。
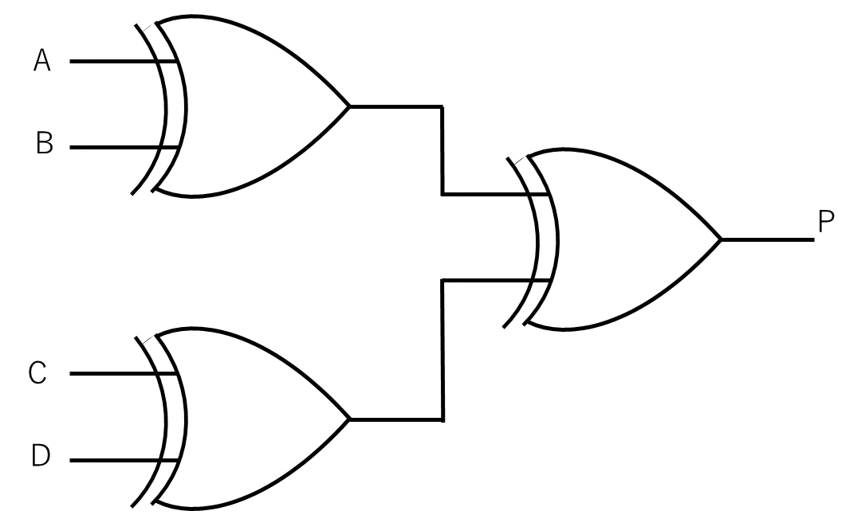
【図9 パリティチェックの回路図】
図9は、A、B、C、Dの4つのビット列のデータから、パリティデータPを作る回路です。
3個の排他的論理和で構成されています。
パリティデータPが“１”の時、奇数、“０”の時、偶数と規定しておきます。
図2の排他的論理和（不一致回路）の真理値表からわかる通り、例えば、AとBが不一致、すなわち“１”の数が奇数の場合は“１”が出力され、同様にCとDが不一致、すなわち“１”の数が奇数の場合は、同じく“１”が出力されると、出力Pには“０”（偶数）が出力されます。また、AとBが不一致（奇数）、CとDが一致（偶数）の場合は、出力Pには“１”（奇数）が出力されます。（下記、図10参照）
【図10 パリティチェックの出力】
このようにして、パリティデータを用いて、データの誤り検出方式に利用することができます。
以上、今回はコンパレータ（比較器）について見てきましたが、コンピュータのデータ処理には、このような回路が多く使われているのです。
（日本アイアール株式会社 特許調査部 E・N)
