【早わかり電子回路】ブール代数の基本をわかりやすく整理 [デジタル回路の前提知識]
今回は、デジタル回路の基礎となる数学、「ブール代数」について説明します。
１．ブール代数とは？
「真（true）」「偽（false）」の2値を取り扱う数学を「ブール代数（boolean algebra）」と呼びます。
「デジタル回路をいかに構成するか？」について考える際、このブール代数の考え方が大変有効なものになります。このことから、ブール代数は論理回路設計の基礎になっています。
ブール代数とは、イギリスの数学者 “ブール” が自身の著書「思考の法則に関する研究」の中で提唱した記号論理学のことです。
ブール代数の基本となる考え方は、真を「1」、偽を「0」で表すことです。
例えば人間は、「浦島太郎は男性である」のような命題の真偽を考えることができます。
この命題は「真」だと考えられますが、それをブール代数では「1」と表します。
ブール代数は，真と偽だけ（1と0だけ）を対象とした代数です。
したがって、1と0だけを対象とした演算を行います。
ただし演算と言っても、加減乗除の四則演算（＋、－、×、÷）ではなく、「AND（論理積）」、「OR（論理和）」、「NOT（論理否定）」という3つの演算を基本とした「論理演算」を行うことになります。
２．論理演算
それでは、3つの論理演算についてみていきましょう。
（1）論理和
2個の変数A、Bについての論理和
F＝A＋B
を考えます。
このような式を「論理式」といいます。
変数A、Bは、２進数なので、０か１のいずれかです。
ここで、変数AとBの組み合わせは、４通りあります。
それぞれの場合の、変数AとBの論理和Fを求めると、次のようになります。
０＋０＝０
０＋１＝１
１＋０＝１
１＋１＝１
最後の行のように、論理演算では、「１＋１＝２」にならずに、「１＋１＝１」となります。
また、この結果を表にしたものをの「真理値表」といいます（表1）。
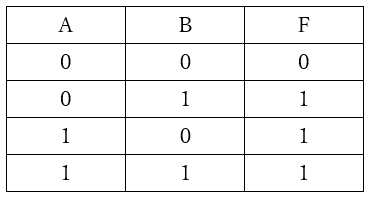
【表1 論理和の真理値表】
論理和は、ORとも呼ばれます。
（2）論理積
2個の変数A、Bについての論理積
F＝A・B
を考えます。
変数AとBの論理積Fを求めると、次のようになります。
０・０＝０
０・１＝０
１・０＝０
１・１＝１
論理積では、全ての変数が１である場合だけ、演算結果が１になります。
論理積は、ANDとも呼ばれます。表2に真理値表を示します。
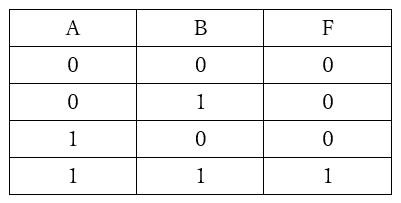
【表2 論理積の真理値表】
（3）論理否定
変数Aについての論理否定は
（Aバーと読みます。）
０と１しかないので、０を否定すれば１に、１を否定すれば０になります。
論理否定は、NOTとも呼ばれます。表3に真理値表を示します。
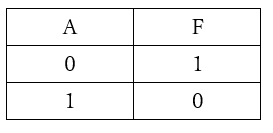
【表3 論理否定の真理値表】
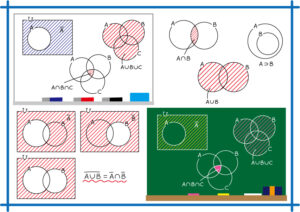
３．ベン図
ベン図とは、集合と集合の関係を視覚的に示す図のことです。
ベン図は集合の関係性を表すもので、集合演算や論理演算を視覚的にわかりやすく表現する手法として用いられています。
論理式を図で表して、視覚的な理解を可能にします。
図1は、変数が1つのベン図です。
図1のように、全体の領域を四角形で表し、変数Aの領域を円とアミで表しています。
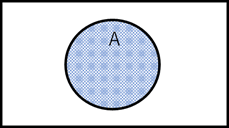
【図1 変数が１つのベン図】
図2は、2つの変数AとBを表すベン図で、全体の領域を四角形で表し、変数Aの領域と変数Bの領域を円で表しています。AとBを重ねることで様々な論理式が表されます。
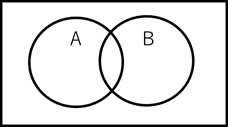
【図2 変数が2つのベン図】
例えば、変数Aと変数Bがあるが、変数Aだけを表す場合は、F＝Aとなり、図3で表されます。
同様に変数Bの否定を表す場合は
となり、図4で表されます。
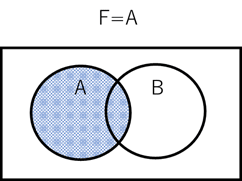
【図3】
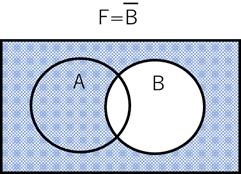
【図4】
上記は、論理否定の場合でしたが、論理和、論理積の場合のベン図は、図5、図6になります。
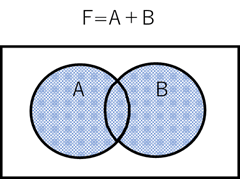
【図5】
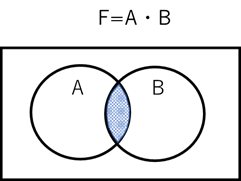
【図6】
さらに、F＝A＋B、F＝A・Bの否定は、それぞれ図7、図8になります
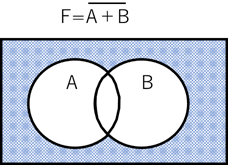
【図7】
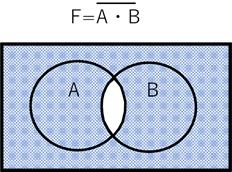
【図8】
４．ブール代数の諸定理
ブール代数の論理式は、通常の算術式と必ずしも一致するとは限りません。
例えば、A＋Aは、通常では、2Aですが、ブール代数では、A＋A＝Aとなります（同一の法則）。
図9にブール代数の諸定理を示します。
【図9 ブール代数の諸定理】
これらの定理は、論理演算を簡単にするときなどに用いられます。
例えば、A・（A＋B）を簡単にしてみます。
A・（A＋B）＝A・A＋A・B＝A＋A・B＝A・（1＋B）＝Aとなります。
ここでは、A・A＝A（同一の法則）、（1＋B）＝1（恒等の法則）を利用しています。
A・（A＋B）＝Aとなって、吸収の法則が証明される結果になりました。
また、ド・モルガンの法則は、真理値表を使って確認することができます。
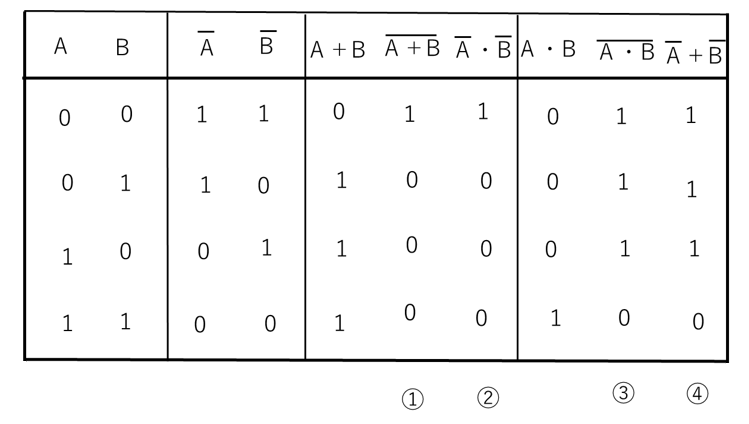
【図10 ド・モルガンの法則の真理値表】
図10は、ド・モルガンの法則の真理値表を示しています。
表から、①＝②、③＝④であることがわかります。
ド・モルガンの法則が証明されたことになります。
５．カルノー図
「カルノー図」は、複雑な論理式を簡単に表記することを目的とした図です。
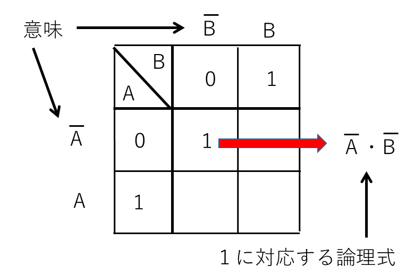
【図11 カルノー図の例】
図11が、A、Bの２変数のカルノー図の例となります。
表の縦横のラベルが、０は論理否定、１は論理肯定となります。
領域に１と記入することで、その領域に対応する論理式が存在することを示します。
カルノー図の作成方法
例として、論理式①＝ 
を、カルノー図を作成して簡略化してみましょう。
論理式の値をカルノー図に表記します。
すると、図12のようになります。
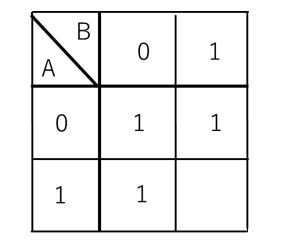
【図12】
カルノー図は、以下の手順に従って、論理式を簡略化します。
- 1が記入されている部分をグループ化
- グループ内の共通項を導き出す
- グループの共通項をまとめて和の式にする
まず、図13のようにグループ化します。
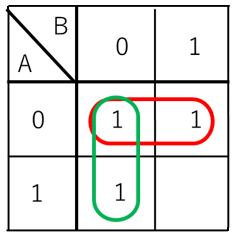
【図13】
共通項は、赤のグループ化がA＝０で、緑のグループ化がB＝０です。
共通項を和の式にすると、
となります。
すなわち、上記の論理式①が簡略化されたことになります。
論理式①のように単純積をOR演算した論理式の形式を「加法標準形」といいます。
論理式をカルノー図で表現するためには、その論理式が加法標準形になっていることが必要です。
変数が4つぐらいまでなら、カルノー図を用いて、論理式を簡略化することができます。
以上、今回はブール代数（論理代数）に関する基礎知識を整理しました。
ブール代数は、デジタル回路の基礎となっている重要なものなのです。
（日本アイアール株式会社 特許調査部 E・N)
