実験計画法とは？誤差の考え方とフィッシャーの3原則
開発・設計や生産の現場においては、コスト削減や納期の短縮が求められる中、実験の効率化は必要不可欠となります。そこで有効な方法として、「実験計画法」と呼ばれる実験計画のしくみがあります。
１．実験計画法とは？
実験計画法は、統計学者のR・A・フィッシャーが農場試験から応用した学問で、効率の良い実験方法の計画を行い、得られた実験データを適切に分析することを目的とする統計学的手法です。
実験計画法を用いると着目する事象・結果にいずれの要因が影響を与えているのか、その要因をどのような値に設定すれば最適かなどを知ることができます。
実験には誤差が伴うため、誤差をできるだけ小さくし、誤差の大きさを推定することが必要となります。
そのためには、フィッシャーによって提唱された原則に基づいて実験する必要があります。
誤差の考え方と原則について実験計画法の基本を説明します。
２．偶然誤差と系統誤差
測定実験を行う場合、実際に収集された測定値と真の値との間にある差を「誤差」といいます。
誤差には、理想的な状況でも測定者がコントロールできない偶然によって生じる「偶然誤差」と、データの収集方法が適切でないため系統的におこるような一定の方向性をもつ「系統誤差」があります（図1）。偶然誤差は測定ごとにランダムにばらつくのに対して、系統誤差は測定の繰り返しに対して一定です。
- 系統誤差の例：測定機械の固有の特性、不十分なキャリブレーション、測定者の一定のくせ、気温・気圧・湿度の変動など
- 偶然誤差の例：測定器の精度限界（読み取り誤差）など
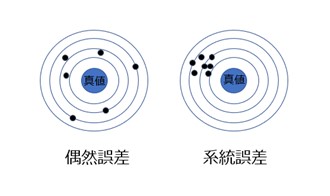
【図1 偶然誤差と系統誤差】
３．フィッシャーの3原則
実験計画法を行う上で、誤差をできるだけ小さくし、誤差の大きさを推定するための3つの原則について説明します。
（1）反復
1回の実験では測定値に違いがあっても、条件による差か誤差なのか判別できません。
同一条件のもと実験を反復することで偶然誤差のばらつきを求めることができます。
（2）無作為化
実験を行う順序や場所を無作為に決めることで、一方的な偏りを生じさせる系統誤差を偶然誤差として処理できます。
（3）局所管理
系統誤差を生じる可能性のある要因によってブロックに分け、各々のブロック内で比較したい条件をすべて入れる方法です。
実験全体を複数のブロックに分割することで、系統誤差を取り除くことができます。
反復により誤差を減らし、誤差の推定をすることができます。
誤差を推定することは、統計的推定や検定に必要となります。
また一方向の偏りを生じる系統誤差はできる限り小さくする必要があります。
無作為化によって系統誤差を偶然誤差に転化し、局所管理によりは系統誤差を取り除きます。
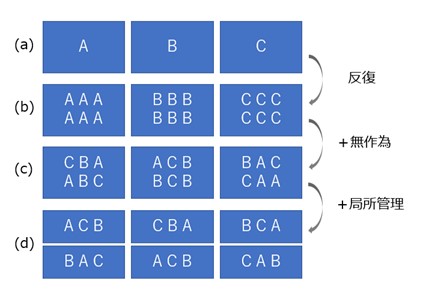
【図2 フィッシャーの３原則】
また、原則の（1）反復と（2）無作為化を満たす場合は、図2(c)の完全無作為化の配置になり、（1）反復（2）無作為化（3）局所管理の3つを満たす場合は、図2(d)の乱塊法という配置になります。
今回は実験計画法の原則について解説しました。
このような原則を意識して、実験計画を行うことで、実験の精度が大きく向上します。
次回は、絶対に押さえておくべき実験計画法の基本用語を解説します。
（日本アイアール株式会社 特許調査部 N・Y)
