【早わかり電子回路】デジタル回路の乗算器・除算器の基本
前回の連載コラムではデジタル回路の加算器と減算器については説明しましたが、今回は「乗算」と「除算」について解説します。
2進数の乗算や除算は、加算器や減算器を用いて計算することができます。
ここでは、デジタル回路で構成される乗算器と除算器について説明していきます。
１．乗算器の仕組みと回路図
まず、乗算の例を考えてみましょう。
2進数の乗算には、次の4パターンがあります。
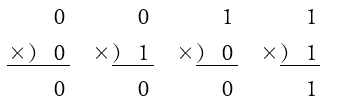
結果は、ANDゲートを通した結果と同じになります。
ここで、2進数の1101×1010を計算してみると（10進数では、13×10）、次のようになります。
上記の筆算のように、一桁づつ左へシフトして加算することにより、乗算することができます。
これをそのまま回路にしたものが、図1に示す乗算器の回路図になります。
乗算は、ANDにより各桁の部分的な積を求め、これらの積を加算するための並列加算器FAを1ビット左にずらして配置しています。
この方式では、乗算時間は高速ですが、積の加算回数に等しい数の並列加算器が必要になり、乗算ビット数が多くなると使用回路規模が増大することになります。
図1は、4ビットの2進数の被乗数A（A３、A２、A１、A０）に乗数B（B３、B２、B１、B０）を掛けた結果の積Z（Z７、Z６、Z５、Z４、Z３、Z２、Z１、Z０）を求める乗算器になります。
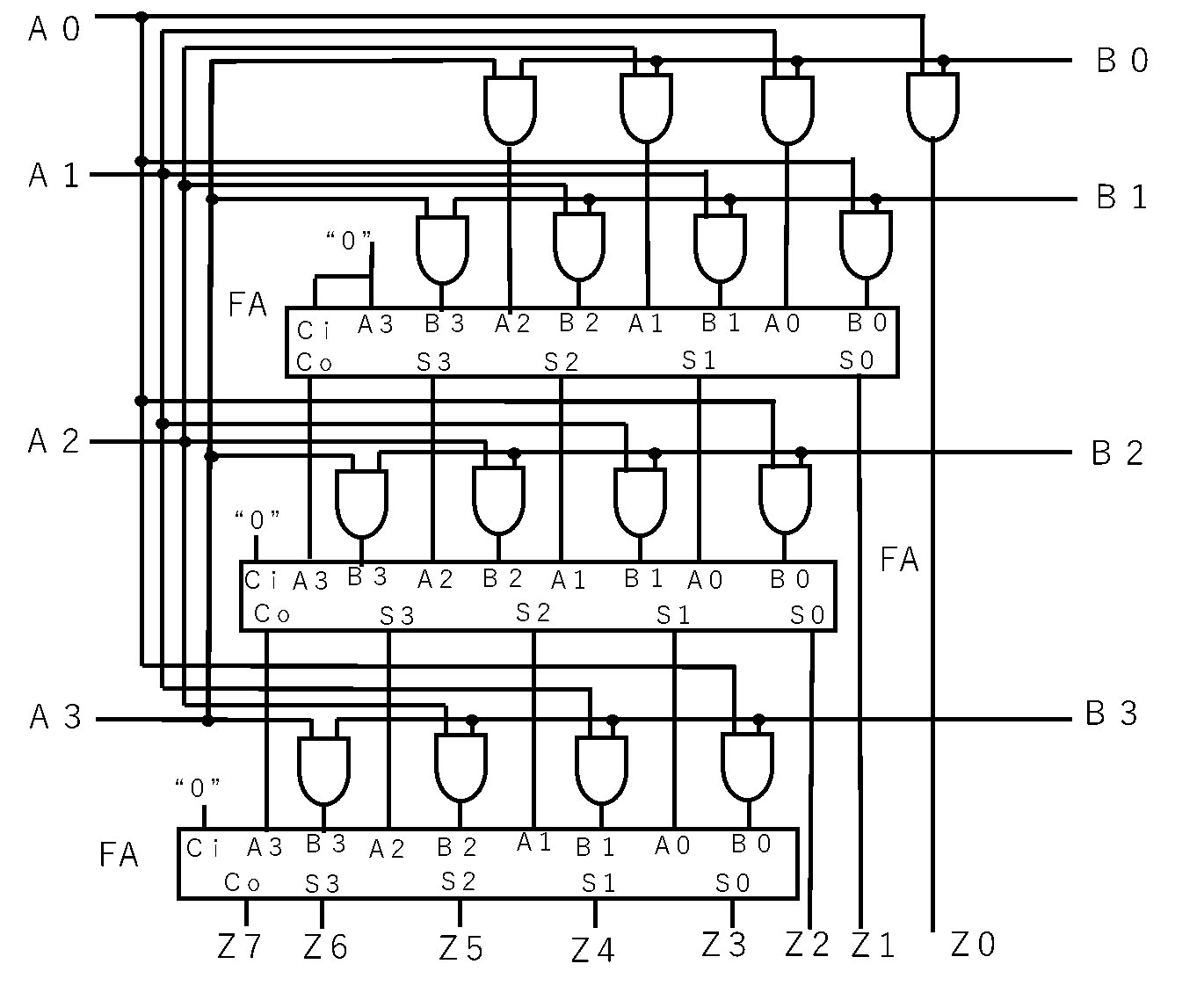
【図1 乗算器の回路図】
２．除算器の仕組みと考え方
論理回路を使って除算を行う方法は、小学校で習った筆算で除算を行うのと同様に考えることができます。
まず、10進数の除算を思い出してみましょう。
例えば、152÷11を計算してみると、次のようになります。
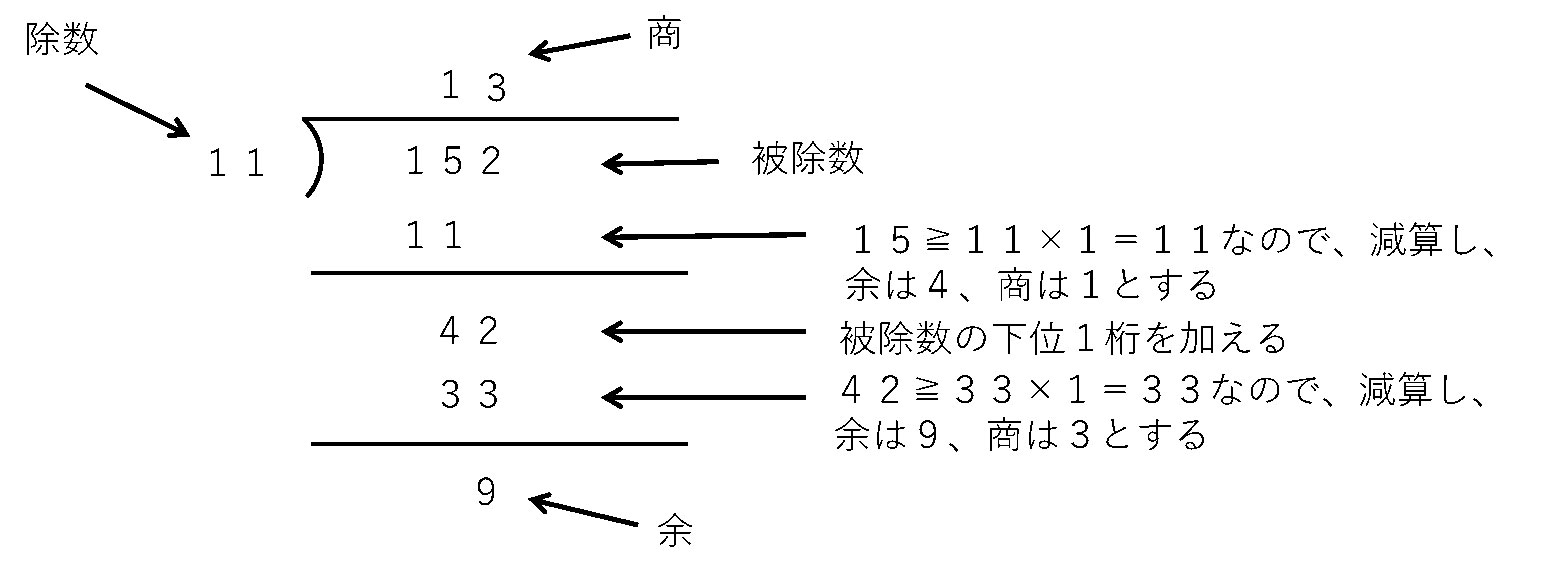
このように筆算で計算し、152÷11=13 余9 となります。
ポイントは、除数を引けるかどうかです。
この例では、被除数の上位2桁から除数が引けるので上記のようになりますが、引けない場合は3桁目も使用することになります。
2進数も同様に考えられます。
例えば、2進数 10101110÷1011 を計算してみます。
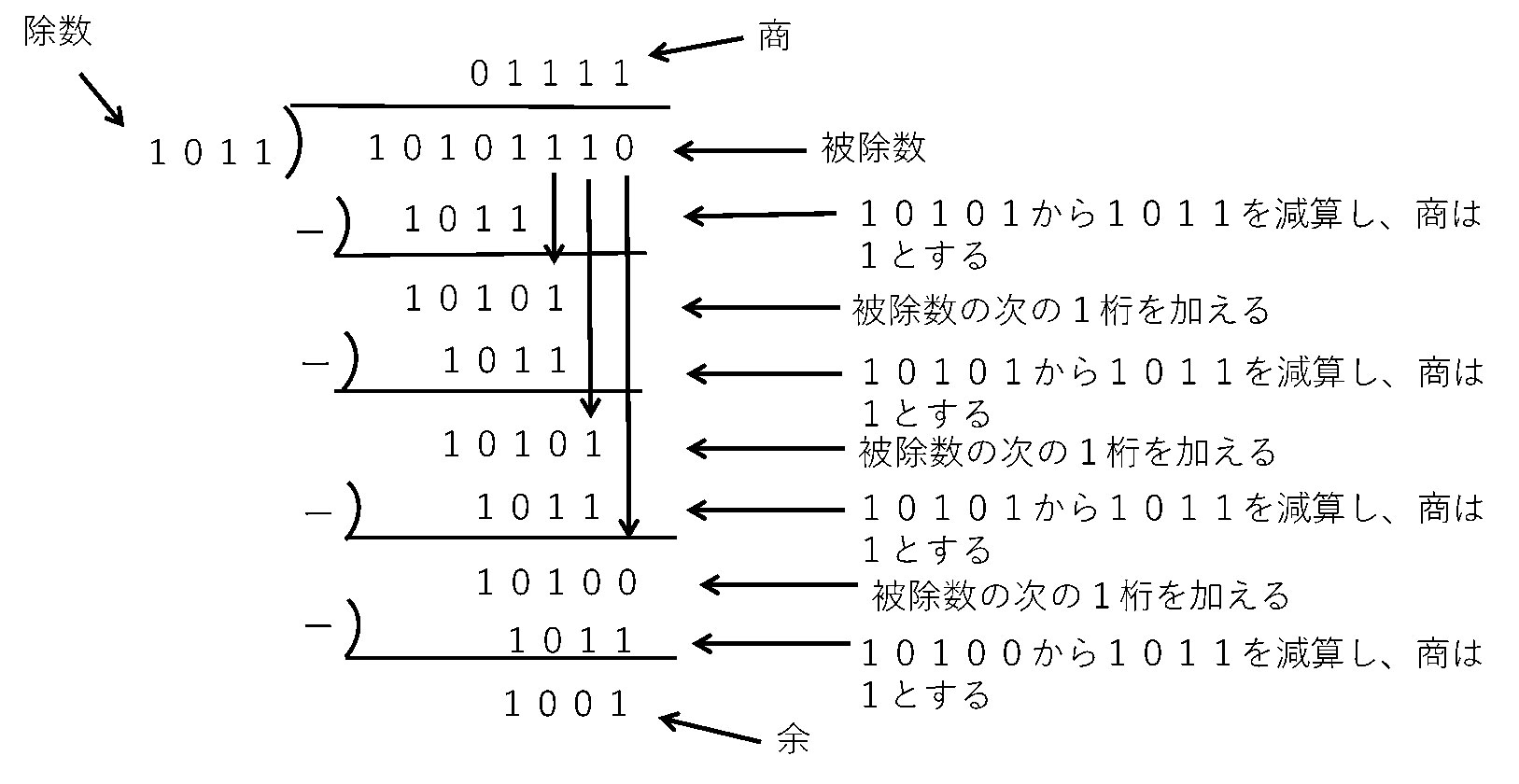
まず、被除数の上位4桁の 1010 と、除数の 1011 を比較します。
1010 から 1011 は引けないので（もし引くと答えは負になってしまう）、商に0を置きました。
次に被除数をもう一桁増やして、10101 から 1011 が引けるかを考えます。
結果は、引けるので、商に1を置き、10101-1011 を計算します。
以下、同様の手順で最下位桁まで計算します。
すると、10101110÷1011=1111 余1001 となります。
10進数では、174÷11=15 余9 となります。
このように、除算は、基本的には、減算をしていけばよいのですが、論理回路では、実際に減算を行ってみて、その結果が正か負かで引けるかどうかを判定することが必要です。
そして、減算結果が正になれば商に1を置き、負になれば商に0を置きます。
減算結果が正か負かは、減算結果の最上位桁を見て判断します。最上位桁が0なら正、1なら負となります。
この方法は、計算の途中で減算結果が負になったときに、値を元に戻すことから「回復法」と呼ばれています。
除算回路は、減算を繰り返し、判定して結果を振り分け、桁シフトが必要になってくるので、除算回路を構成しようとすると非常に複雑になってしまいます。（ここでは、回路図は割愛します。）
実際は、除算のための様々なアルゴリズムがあり、ソフト的に処理されることが多いです。
（日本アイアール株式会社 特許調査部 E・N)
