分散分析の基礎 「ばらつき」の考え方がスッキリわかる！
連載「これならわかる実験計画法」の統計編2回目は、分散分析を理解するために必要となる「ばらつき」の概念について解説します。
１．「ばらつき」とは
買った桃からお店の桃の特性を推定できそうなのはわかりましたが、甘い桃を選ぶ基準を決めるには、他に何がわかればよいでしょうか？
色の違いを無視して、サイズごとの糖度をグラフで見ると（図1）、データがばらついているため、サイズによって糖度が本当に違うかよくわかりません。ばらつきについても考える必要がありそうです。
ばらつきには、糖度を測定する時の誤差などがありますが、その他にもばらつきの原因はないでしょうか。
サイズは大雑把に大、中、小としか分けていませんから、サイズという要因がばらつきに影響を与えていることは間違いありません。また、色の違いもばらつきの原因になりえます。
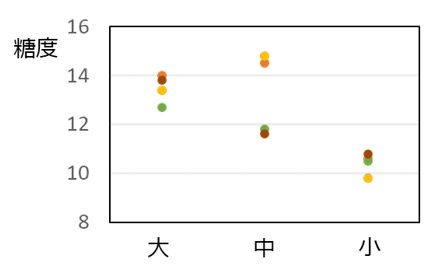
【図1 桃のサイズと糖度】
２．ばらつきの指標：標準偏差
ばらつきを扱うときに、ばらつきの程度を表す指標があると便利です。
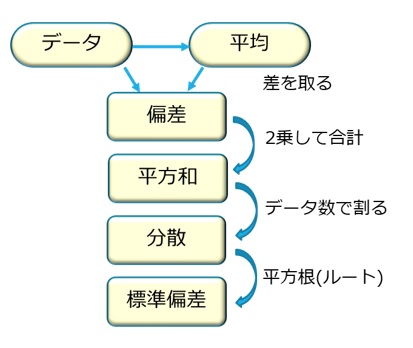
各データが平均値からどれくらい離れているかは、各データと平均値の差（偏差）であらわせますが、偏差を単に合計しただけでは正負が相殺されて0となるので、全体のデータがどれくらいばらついているのかを示すことができません。
そこで、偏差を2乗してすべて合計した「平方和」を取ります。データが増えると平方和は大きくなるので、平方和をデータ数で割った「分散」、分散の平方根をとり偏差と単位をあわせた「標準偏差」という指標で、全体のデータが平均値からどれくらいばらついているかを表します。
ここからの説明でも、具体的なイメージをもっていただくために、当連載コラムの前回「《実験計画法と統計》推定と仮説検定の考え方」で紹介した桃のサイズ、色と糖度のデータを用いて、サイズの水準ごとに実際に計算をやってみましょう。
色の違いを無視して、サイズごとの糖度をグラフにしたのが上記図1で、表1はグラフのもとになる、サイズ、色と糖度のデータです。
【表1 桃のサイズ、色と糖度】
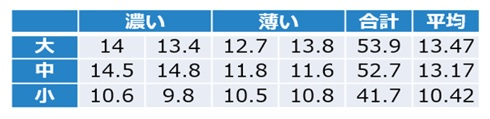
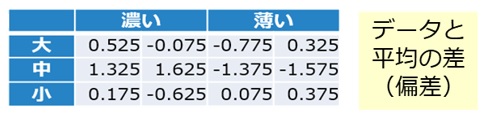
表1からデータと平均の差（偏差）を計算します。
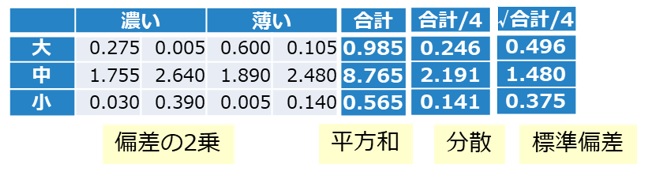
さらに、偏差の２乗、平方和、分散、標準偏差を計算します。
こうして計算した標準偏差を、図1の平均値の上下に赤矢印（長さは標準偏差の２倍）で示しました（図2）。
ばらつきの指標になっていることが実感できるのではないでしょうか。
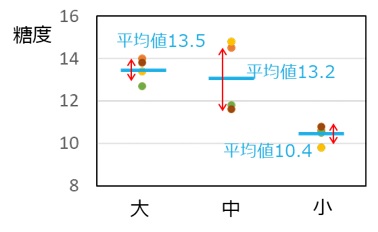
【図2 桃のサイズと糖度のグラフに平均値と標準偏差を記入】
３．ばらつきの仕組み
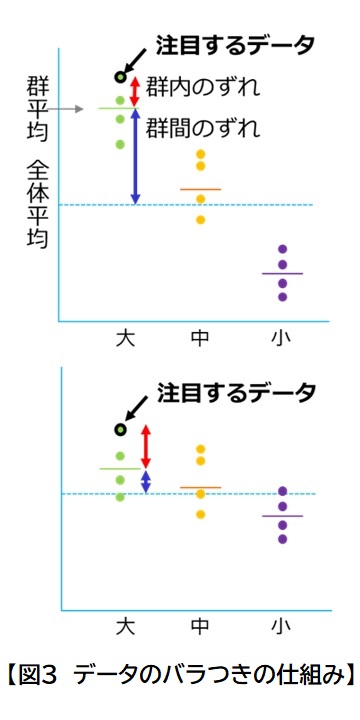
桃のサイズに注目した時のばらつきについてもう少し詳しく考えます。
図3の「大」のデータの1つに注目してみると、全体の平均値と「大」のグループ（群）の群平均値とのずれ（群間のずれ）と、「大」のグループ内でのずれ（群内のずれ）を合わせたものが、全体平均からのずれになります。
これはすべてのデータで同じで、
全体平均からのずれ＝群間のずれ＋群内のずれ
と記述することができます。
上と下の図を比べると、上の図のように群間のずれが群内のずれより大きければ、サイズによる違いがあると言えそうですが、下のような図の場合、サイズによる違いがあると言えるかどうか、微妙です。
実際に違いをもっともらしく比べるにはどうしたらよいでしょうか？
群間のばらつき（分散）と、もともと全体のデータに含まれる誤差のばらつき（分散）を比較すれば、サイズによる効果を調べられそうです。
そこで、データのばらつきが
- 因子（サイズ）によって起きているものなのか、
- 本来の誤差によって起きているものなのか、
を調べる「分散分析」という方法があります。
ここで、「本来の誤差」と言っていますが、注目している因子以外の原因によるばらつきは、すべて誤差とみなされることに注意して下さい。
例えば、色によって桃の糖度に違いがあったとしても、サイズにのみ注目し、色に注目しなければ、色による違いは誤差として扱われることになります。
（日本アイアール株式会社 H・N)
