評価サンプルの「実験前の取得データ」を軽んずべからず（技術者べからず集）
製品やシステムの開発では、機能・性能評価や信頼性評価などの実験評価が必要となりますが、評価サンプルに対して実験前に取得する前データについて注意しなければならない点について考えてみましょう。
目次
１．実験後のデータ
実験前データの前に、実験後のデータについて考えたいと思います。
実験には様々な目的に対して、評価が行われ、評価サンプルの数が多くなることがあると思いますが、全てのサンプルに対して、同じ項目について実験後データを採取するのは意味がありません。（評価サンプル数と項目数が極めて少ない場合は別ですが）
例えば、劣化を評価するテストでは、前データの無い場合には劣化量を評価することはできないため、後データを取ることは無意味です。
ただし、市場での実際の劣化を評価するためにデータを取得する場合には、初期値として出荷規格値を用います。この場合に評価・判別が可能なのは大幅な想定外劣化のみです。
基本的には、前データの有る項目・ポイントにおいてテスト後データを測定しますが、前データが有っても、テスト内容が、評価変数に関係ないものの場合も後データの意味はありません。例えば電磁ノイズのテストを行ったものに対して性能劣化項目の評価は必要ありません。
２．実験前のデータ
実験後のデータが実験前のデータ採取に基づくとすると、前データをどのように採取するのかの計画が重要となります。
評価の目的をはっきりさせ、前データと後データでどのような分析を行うのかを考える必要があります。
開発時の機能・性能評価では、仕様や工程の変数の影響を評価します。
信頼性評価では、ワーストケースサンプルを試作して耐久テストを行い、仕様や工程の機能・性能劣化への影響を「実験計画法」や「タグチメソッド」など用いて多変量解析を行います。
評価は面で行うことはできず、網の目のような評価ポイントをどのように設定するのかを考えなければなりません。単純な等間隔の評価ポイントの設定では正しい知見が得られない場合があります。
一方、ひたすら網の目を細かくするような評価ポイント設定では、評価工数が膨大になります。
３．評価ポイントの設定と実験後データの解析
評価ポイントの設定にあたっては、バラツキの考慮と定性（特性）の理解が重要です。
シミュレーションなどによる定性の理解と、実験による定量値の確認は真の現象をつかむうえで、車の両輪のようなものです。
次より模式図を用いて、考え方を説明します。
実際の評価結果には、変数以外に製品のバラツキや変数以外の因子やテスト条件のバラツキ、そして実験における測定精度が影響します。
理解のために、正しい値を「真値」と呼び、測定値のバラツキ幅との関係を示すと図（A）のようになります。
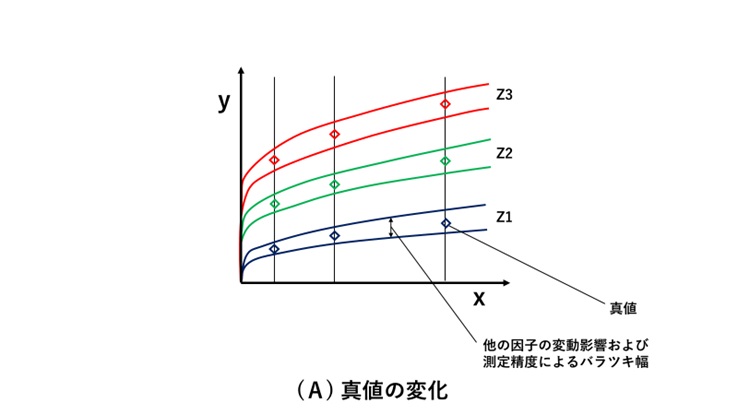
曲線で示したのは、「理解されている定性（x、zの変化に対するyの変化特性）」です。
実際の測定値は、真値に対して、バラツキ幅の中に評価結果として得られます。
上記の図（A）を念頭において、評価ポイントの設定が不適切な例を二つ説明します。
変数xの実験幅が不充分な場合の例
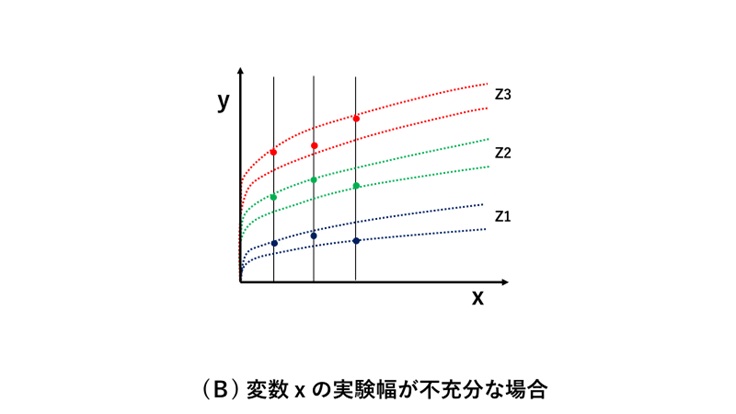
図（B）は変数xの実験幅が不充分な場合です。
青、緑、赤の各点は測定値を示しますが、このような結果から、図（C）のようなグラフを作成しても、図（A）の特性とは全く異なることが分かります。
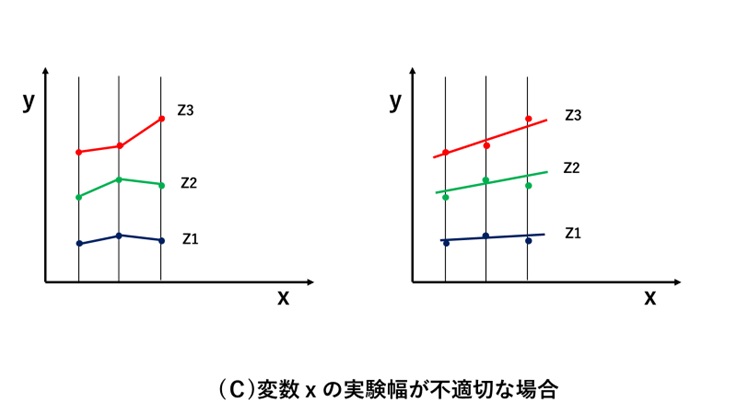
バラツキの考慮が不足していて不適切な例
次に挙げる不適切な評価ポイント（変数）の設定例は、バラツキの考慮が不足している場合です。
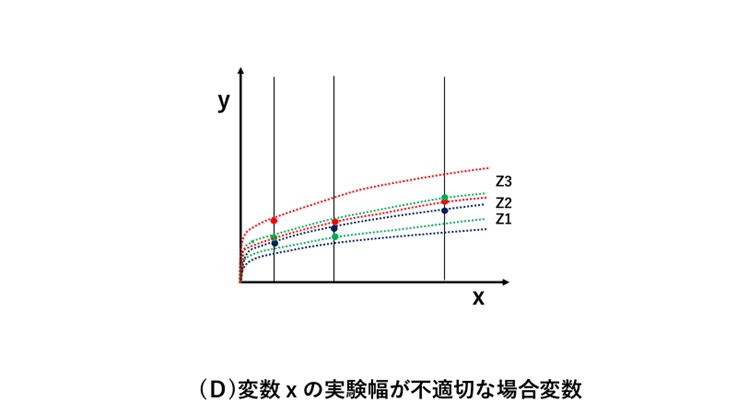
図（D）に示すように変数ZをZ1～Z3と変化させ測定をしていますが、実際の測定値はバラツキの影響を受け青、緑、赤のようになります。
このような測定結果を基にグラフ化すると、図（E）のようになり、定性も分からない上に、変数zの影響において上下逆転が生じます。
変数の実験幅が適切な場合の例
一方、以下図（F）は、変数x、zの実験幅が適切な場合の実験結果を示しています。
変数xの評価点も単純な等間隔ではなく、想定される定性（特性）に基づいています。
参考に図（A）の「真の」状態を、破線で示しました。実測値は「真値」に対して、図（F）の青、緑、赤のようになります。
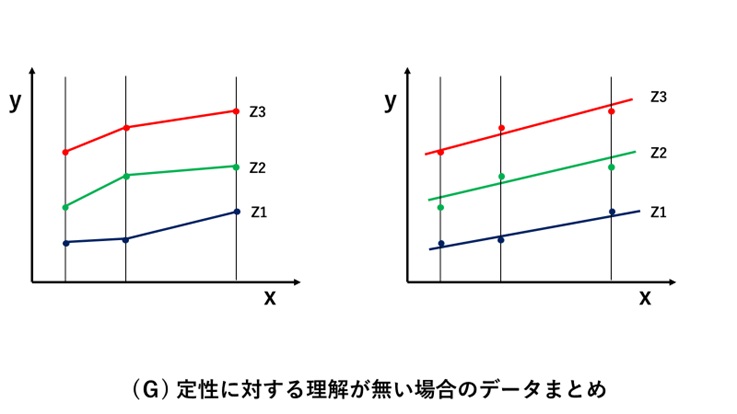
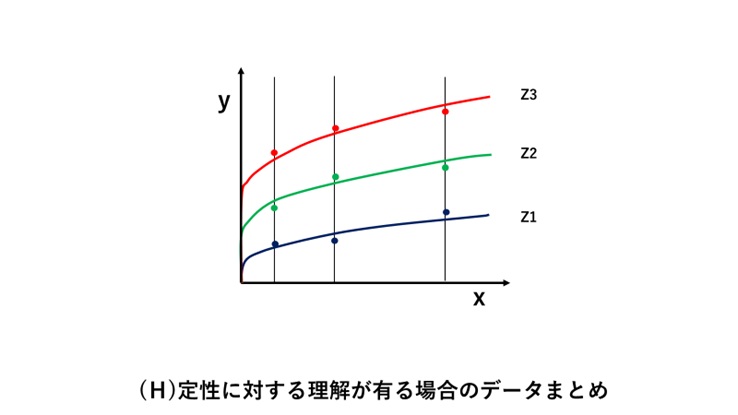
図（F）の実験データのグラフ化において、定性（特性）が理解できている場合には、以下図（G）のようになることはなく、図（H）に示すように、一次データ（測定データ）を適切に解析ができます。
４．二次解析グラフの活用
信頼性の評価においてワーストケースサンプルを試作しようとしても、狙って作る場合には極めて狭い製造公差のもの試作が必要で、一方選別する場合には大量の試作が必要となります。
一方、図（H）のグラフができれば、得られた影響感度や外挿を用いて図（I）の紫のようなポイントK（ワーストケースポイント）が得られます。
変数yが負荷である場合には、強度限界と比べることにより、このポイントの変数条件での強度余裕率が求まります。
図（I2）のように、適用範囲に予定していたポイントKが強度限界を越える場合には、目標余裕率を基に、黄色エリアのように、x、zに制限を加えた新たな適用範囲を求め、「見える化」もできます。
５．仕様履歴の管理と評価
仕様や工程を変更する場合には、仕様履歴に基づいた適切な評価サンプルを試作し、図（I）に基づき、評価ポイントの設定や評価方法の計画を行わなければなりません。
仕様や工程に対しても、評価目的に応じた前データを残さないと、思わぬ外乱で評価結果の理解ができなくなります。
（知らない間に仕様や工程が変更されていた試作サンプルを知らずに評価してしまったというのは論外です）
仕様管理をしっかりし、定性に関する理解を深め、適切な評価点に対して、効率的な実験評価と分析を行いましょう。
（アイアール技術者教育研究所 H・N)
