多変量解析に必要な統計基礎を解説！データのばらつき/正規分布/3σルールと分散
多変量解析では、回帰式やモデルの形だけでなく、データのばらつきをどう捉えるかが結果の解釈を大きく左右します。
本連載の第3回となる今回は、回帰分析やデータの種類といった前回までの内容を踏まえ、データのばらつき・正規分布・3σルール・分散といった統計の基礎概念を整理します。
分析結果を正しく判断するために押さえておきたいポイントを具体例とともに解説していきます。
１. 回帰分析とデータのばらつき
回帰分析を利用して現象の原因（「説明変数」と呼ばれる）と現象の結果（「目的変数」と呼ばれる）の関係を直線で表現した場合、図1のように測定したデータ（●印）は回帰直線（破線）上にきれいに並ばずに乖離が観測されます。図1では投入量が説明変数、生成量が目的変数です。図中に回帰直線の式と決定係数（R2）の値も記載されています。
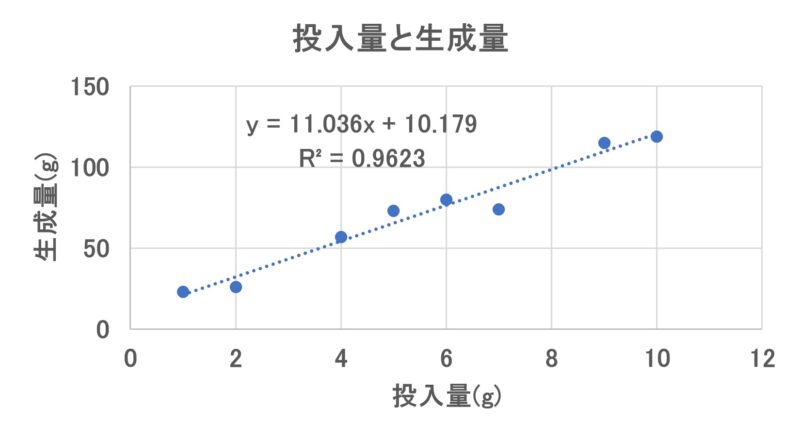
【図1 説明変数と目的変数】
「決定係数（coefficient of determination）」は「R2」とよく略記されます。係数の値が1であれば回帰直線からの誤差は全くなく、値が1から小さくなるほど誤差が大きいことを示す指標になります。
決定係数は一つの数値だけで複数のデータの平均的な誤差の大きさが判断できる点はとても便利ですが、実はデータごとのばらつきを調べてみることもとても重要です。
図1では各投入量に対する生成量は一つの●印で示されていますが、同じ投入量で何回か測定しその「平均値（mean value）」のみを採用することが多いでしょう。
２. データ分布と正規分布の考え方
話を簡単にするために、投入量を5(g)に固定して、何度も生成量を測定しその分布を調べてみます。
図2は生成量とその生成量が現れる頻度をプロットした図です。2本の曲線が描かれています。両方とも平均値は73（図中の垂直な直線）で同じですが、「標準偏差（standard deviation）」が2 （黒色の実線）と6 （赤色の破線）のケースにそれぞれ対応した頻度曲線になります。生成量が投入量だけで一意に決まり測定誤差も全く無い理想的なケースでは測定される生成量は、いつも73（図中の垂直な直線に対応）になるはずです。図中の2つの曲線のように生成量が分布を持つ場合は、何か別の要因が存在するか、あるいは単なる測定誤差だと考えられます。
分布の原因が測定誤差だけであると考えられる場合には、その分布は「正規分布（normal distribution）」あるいは発見者の名前を取って「ガウス分布」に従うことが知られています。
少し専門的になるのでこのコラムでは紹介しませんが、測定した誤差の分布が正規分布に従うかどうかをさらに調べたい場合は「Q-Qプロット」を描く、あるいは「正規性の検定」を実行する手段というのもあります。
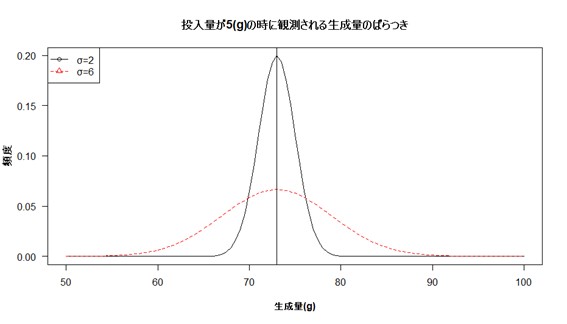
【図2 正規分布の例】
３. 3σルールと外れ値の解釈
分布が正規分布に従うと仮定した場合に、毎回測定した個々のデータがもっともらしい値であるかどうかを判定する基準として統計あるいは品質管理分野で「3σ（3シグマ）」がよく利用されます。σはデータの広がりを表現している「標準偏差」のことです。
データ分布からその平均値および標準偏差（σ）をまず計算します。
次にデータの下限値（平均値-3σの値を計算する）および上限値（平均値+3σの値を計算する）として、その区間にあるデータは図3の緑色の領域にあります。
赤の破線の下の面積に対して緑色の領域の面積は99.7%になります。言い換えるとデータ測定を繰り返した場合に99.7%の確率で測定データは（平均値-3σ）と（平均値+3σ）の間の区間に入ります。99.7%という数字を別の表現で説明すると、測定データがその区間に入らない場合は300回に1回程度しか現れないデータであり、緑色の領域に入らない場合には別の要因があって値がはずれたのかもしれないという考え方ができます。
このはずれたデータを「はずれ値（outlier）」と呼ぶことがあります。「箱ひげ図（boxplot）」という手法で可視化することもできます。
この解釈をもっと知りたい場合はさらに統計・検定の勉強をする必要があります。
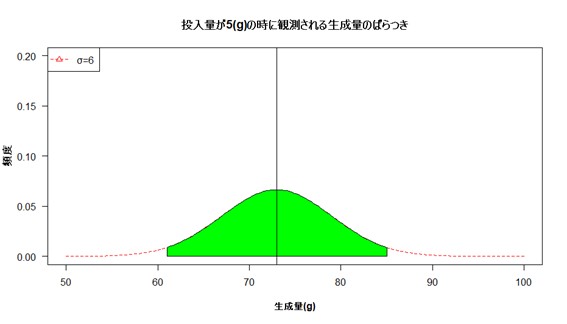
【図3 正規分布とはずれ値】
４. 分散とその実用的な性質
「分散（variance）」は標準偏差を二乗した値です。今回のように、生成量[g]が変数である場合、分散の単位は[g2]となりますが、標準偏差の単位は元の変数と同じく[g]になりますので数値としての判断がしやすいというメリットがあります。
このように説明すると、分散は標準偏差を計算する途中の過程で出てくる数字と思われるかもしれませんが、理論を検討する上では標準偏差よりも分散を基準に考えることの方が多いことを覚えておきましょう。
分散の加法則
最後に、分散に関して実用上知っておくととても便利な法則がありますのでそれを紹介します。
以下の具体的な問題を解いて理解を深めましょう。
【質問】
ある製品を製造するために3工程（A,B,C）を順次通過する必要があります。
A工程の所要時間は平均35[秒]、標準偏差10[秒]、B工程の所要時間は平均30[秒]、標準偏差7[秒]、C工程は毎回10[秒]です。
A,B,C工程の所要時間はお互いに無関係だとすると全体の所要時間の平均値および標準偏差はいくらでしょうか？
まず平均値は簡単ですね。
平均値 = 35 + 30 + 10 = 75 [秒]
次に標準偏差ですが、以下の式にはなりません。
標準偏差 = 10 + 7 + 0 = 17 [秒]
お互いに独立な変数の分散については以下の「分散の加法則」が成り立ちます。
変数（X+Y+Z）の分散 = 変数Xの分散 + 変数Yの分散 + 変数Zの分散
今回の3変数の分散和をまず計算すると、
10×10 + 7×7 + 0×0 = 149
となり、149の平方根を取って標準偏差を計算すると、12.2 となります。
したがって求める標準偏差は12.2 [秒]です。
標準偏差に加法則が成り立つのではなく、分散について加法則が成り立つのです。ただし「分散の加法則」が成り立つのは、変数が互いに独立であるという条件下であることを忘れないようにしましょう。もし成り立たない場合は、製品ごとにトータルの所要時間をまず計算し、それらのデータの平均、分散および標準偏差を計算する必要があります。
５. おわりに
本記事では、多変量解析を理解するための統計基礎知識として、データのばらつきや正規分布、3σルール、分散といった考え方を整理しました。これらは分析手法そのもの以上に、得られた結果をどのように解釈し、判断につなげるかを左右する重要な要素です。多変量解析を実務で活用する際には、数値の背後にあるばらつきや誤差の存在を意識しながら、分析結果を読み解くことが求められます。
（アイアール技術者教育研究所 A・T)
