デジタル回路の加算器・減算器の仕組みをわかりやすく解説

コンピュータは「電子計算機」とも呼ばれますが、どうやって計算しているのでしょうか?
コンピュータはデジタル回路で構成されているため、計算もデジタル回路によって行われます。
ここでは、デジタル回路で構成される加算器と減算器について解説します。
1.加算器の仕組みと回路図
デジタル回路における加算器は、2進数の加算を基本として構成されています。
まずは、半加算器と全加算器について見ていきましょう。
(1)半加算器
2進数の加算はどのようにされるのでしょうか?
まず、2個の1ビットデータ(2進数)の足し算を考えてみます。
足し算の組み合わせは、次のようになります。
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
ここで、1+1の場合は、答えは、1桁目の0で、2桁目に1が桁上げしたと考えます。
これを真理値表にすると、図1のようになります。これを「半加算器」といいます。
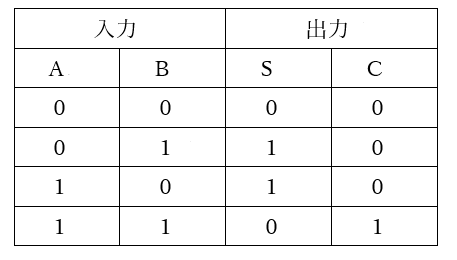
【図1 半加算器の真理値表】
図1において、AとBとSについてみると、XOR(排他的論理和)の関係になっていることがわかります。
次に、AとBとCについてみると、ANDの関係になっていることがわかります。
すなわち、回路図であらわすと図2のようになり、また、図記号で表すと図3になります。
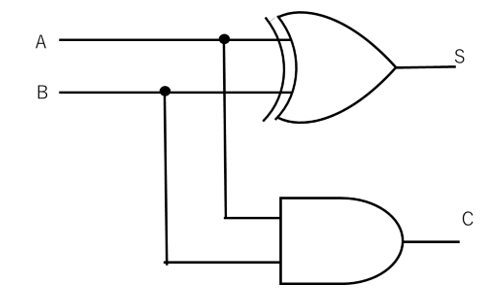
【図2 半加算器の回路図】
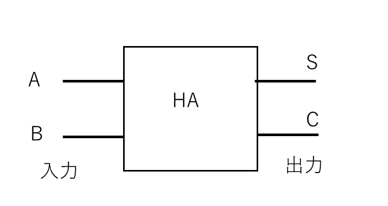
【図3 半加算器の図記号】
半加算器は、1桁の加算をおこない、上位のビットに桁上げ信号を与えることができます。
しかし、下位のビットからの桁上げ信号は、受け取ることができません。
つまり、半加算器は1桁だけの加算しかできないものなのです。
(2)全加算器
そこで、上記のような問題を解決するために用いられるのが「全加算器」です。
全加算器は、上位の桁に桁上げ信号を与え、下位の桁からの桁上げ信号を受け取れるようにしたものです。
半加算器に、下位ビットからの桁上げ信号を受け取る機能を加えたものが全加算器です。
計算としては、足される数(A)と足す数(B)と下位からの桁上げ信号(C0)の3個のデータを加算します。
そして、和(S)と上位桁への桁上げ信号(C1)の2個のデータを出力します。
その真理値表を図4に示します。
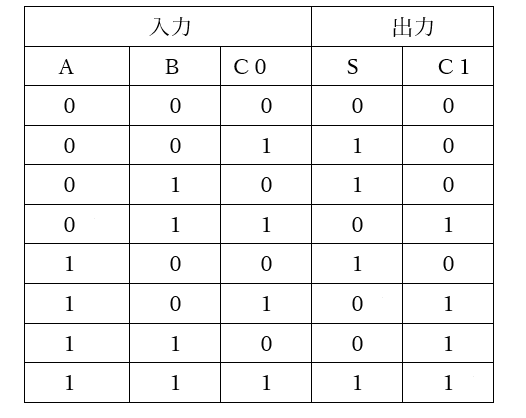
【図4 全加算器の真理値表】
また、図5は、半加算器を用いた全加算器の回路図で、図6は図記号となります。
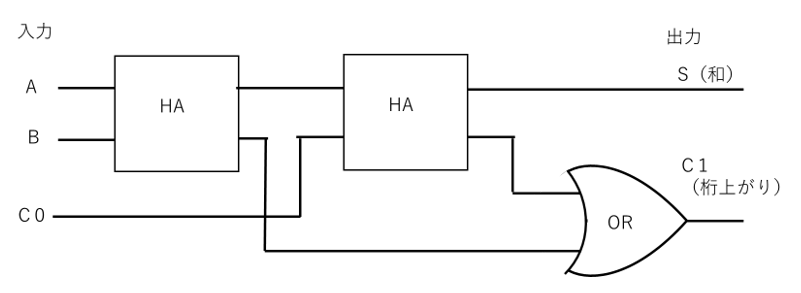
【図5 全加算器の回路図】
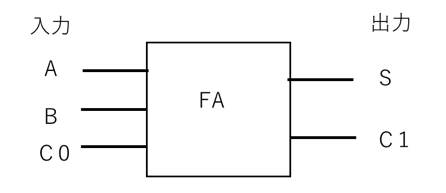
【図6 全加算器の図記号】
次に、具体的な全加算器の計算を見てみましょう。
例えば、10進数の6+11を計算してみると、まず、10進数を2進数に直し、

のように置き換えます。
1桁目を半加算器、2桁目以降を全加算器で加算すると、図7のように計算できます。
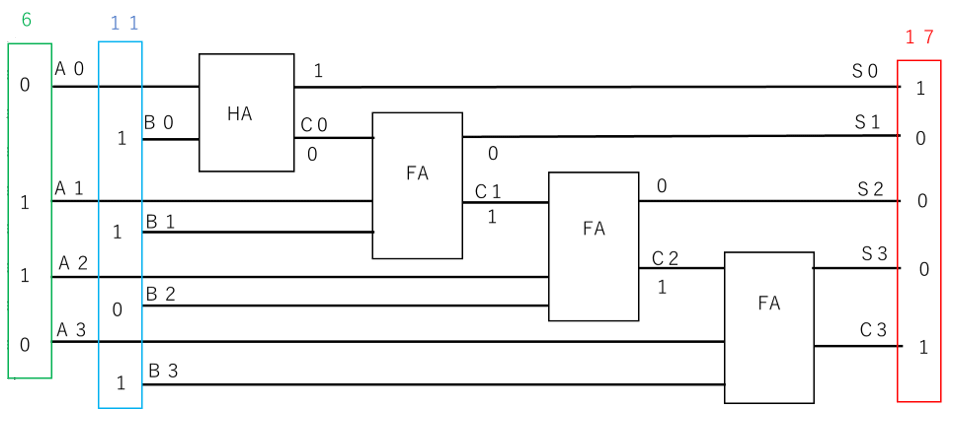
【図7 全加算器の回路(例)】
具体的には、A0の0と、B0の1を足すと(半加算器に入力)、S0(和)が1になり、C0(桁上がり)は0になります。次に、A1の1と、B1の1と、C0の0を足すと(全加算器に入力)、S1(和)は0で、C1(桁上がり)が1になります。
というように、次々に加算器に入力していくと、和(C3、S3、S2、S1、S0)が求まります。
したがって、以下のようになります。(10進数では、17)
![]()
このように、2進数の桁数だけ全加算器(1桁目は半加算器でも可)を並べれば、加算ができます。
2.減算器の仕組みと回路図
減算も加算と同様に、基本的な論理回路を組み合わせることで実現できます。
ここでは、半減算器と全減算器について説明します。
(1)半減算器
減算の場合も、加算器と同様に、まず「半減算器」を考えてみます。
2個の1ビットデータ(2進数)の引き算を考えてみます。引き算の組み合わせは、次のようになります。
0 - 0 = 0
0 - 1 = 1
1 - 0 = 1
1 - 1 = 0
ここで、0-1の場合は、答えは、1で、2桁目から借りが行われたと考えます。
これを真理値表にすると、図8のようになります。これが「半減算器」です。
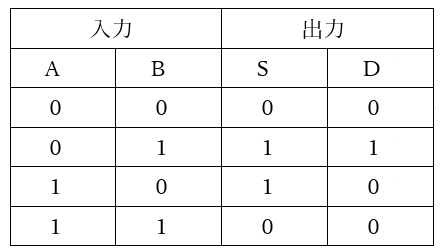
【図8 半減算器の真理値表】
図8の真理値表を回路図であらわすと、図9のようになります。
また図記号で表すと図10になります。
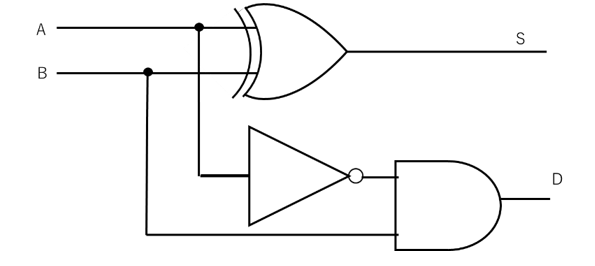
【図9 半減算器の回路図】
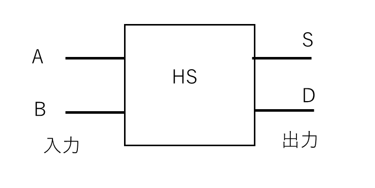
【図10 半減算器の図記号】
半減算器は、下位の桁からの借り信号を受け取ることができません。
したがって、半減算器は、半加算器と同様に1桁だけの計算しかできません。
(2)全減算器
次に、「全減算器」を考えます。
全減算器は、上位の桁に借り信号を与え、下位の桁からの借り信号を受け取れるものになります。
計算としては、引かれる数(A)と引く数(B)より計算した仮の答えから、さらに下位からの借り信号(D0)を減算します。そして、差(S)と上位桁への借り信号(D1)の2個のデータを出力します。
その真理値表を図11に示します。
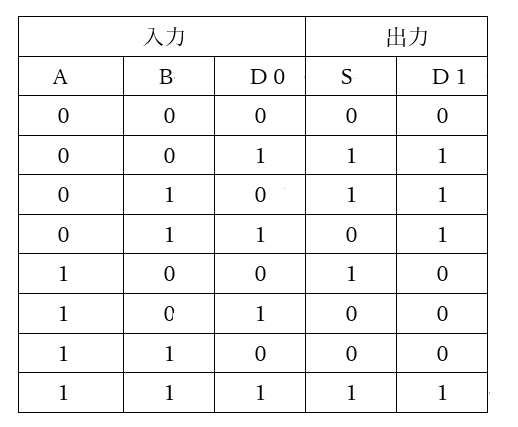
【図11 全減算器の真理値表】
また、図12は、半減算器を用いた全減算器の回路図で、図13は、図記号となります。
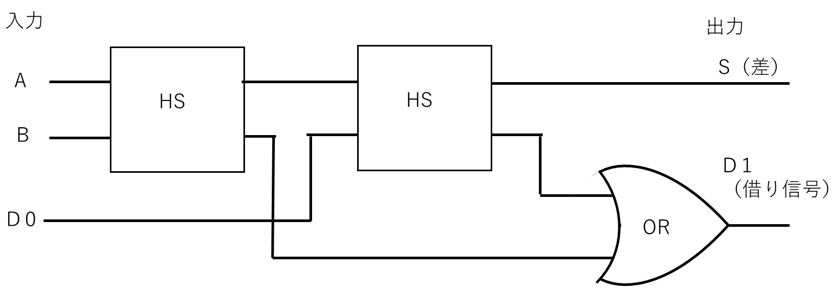
【図12 全減算器の回路図】
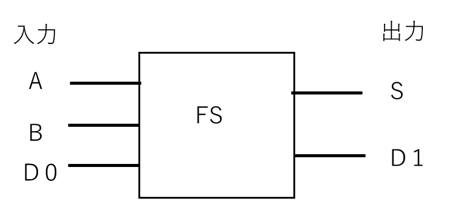
【図13 全減算器の図記号】
具体的な引き算をした場合の図を図14に示します。
10進数の9-6を計算すると、以下のようになります。

回路は、加算器の接続の場合と同様に考え、図14のようになります。
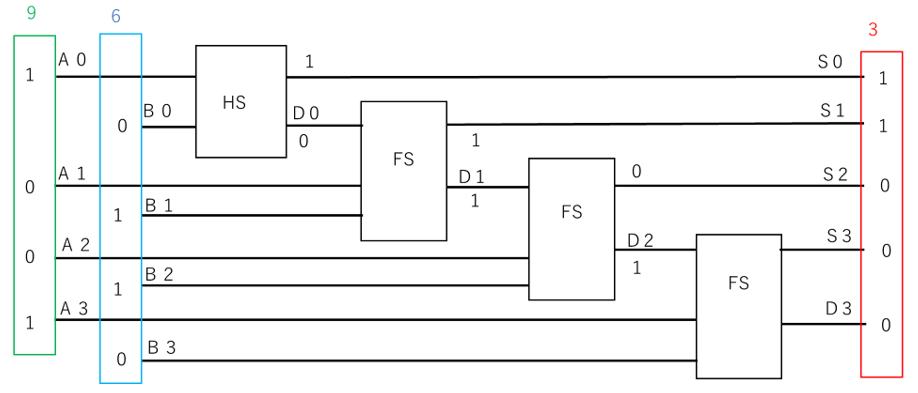
【図14 全減算器の回路(例)】
以上のような、デジタル回路での加算と減算はコンピュータにおける計算の基本となっており、とても重要な前提知識です。しっかりと理解しておきましょう。
次回は、続きとして乗算器と除算器の仕組みを解説します。
(日本アイアール株式会社 特許調査部 E・N)














](https://engineer-education.com/wp/wp-content/uploads/2021/10/electric-circuit-dc0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2021/10/Circuit-element0-150x150.png)































