【QC検定4級対策】サンプリング、ばらつき、平均の概念

QC検定は、JSA日本規格協会グループが主催する品質管理の知識を問う筆記試験です。
内容は品質管理とは何か？から始まり、改善活動の基礎知識、統計的なプロセス管理など多岐にわたります。
受験者数は年々増加しており、毎年の受験者数が10万人を超える製造業ではメジャーな試験です。
［※関連記事：【技術系資格ナビ】QC検定（1〜4級の難易度/合格率/勉強方法/メリット）はこちら］

この連載では、各級の頻出範囲について例題を交えて解説を行います。
この連載を通じて、QC検定の受験準備をしてみましょう。
まずは学生や新社会人を対象とした4級試験について3回に分けて解説します。

4級の出題範囲はJSAグループのHPで公開されている「品質管理検定（QC検定）4級の手引き」（全48ページ）に限られています。しかし、受験に不安を覚える人はぜひ例題を解いて、実践に備えましょう。

【4級解説：第1回】サンプリング、ばらつき、平均の概念
今回のまとめ

【4級解説：第1回】サンプリング、ばらつき、平均の概念

「品質管理検定(QC検定)4級の手引き」から「2.2事実とデータに基づく判断」の章を2回に分けて解説します。母集団、ばらつき、ランダムサンプリングなど聞きなれない言葉が多いかもしれませんが、例題を通じて用語の解説も行いますので、早速下記の例題について考えてみましょう。

例題

《問題》
母集団の性質について調べるために、ランダムサンプリングを行った10個のアルミ部品の強度試験結果(データ)を下表のとおり調べた。このデータを用いて母集団の傾向をつかもうとするとき、もっとも適切だと思われるものはa～eのうちどれか。

QC検定4級の例題

a. 平均値xだけを調べる。
b. 中心値(メディアンx)だけを調べる。
c. 範囲Rだけを調べる。
d. ランダムサンプリングを行ったので、データには全くばらつきがない。
e. データは必ずばらつくので、平均的(中心)傾向とばらつき傾向の両面を検討する。

《解答》

解答例はここをクリック

e.データは必ずばらつくので、平均的(中心)傾向とばらつき傾向の両面を検討する。

問題文について［母集団／サンプリング／サンプル］

解答の解説の前に、まずは問題文の解説をします。

この問題で調査したいのは母集団の傾向です。母集団が何かは問題文には明確に書かれていませんが、例えば「その日工場で製造したアルミ部品全ての強度試験結果」とします。出荷前に強度が十分かどうか確認するために母集団の傾向を知りたいと考えている、と想像してみましょう。

しかし強度試験は破壊試験（試験すると壊れてしまう）なので全ての部品を試験することはできません。このような場合商品となる部品とは別に、試験するアルミ部品を何個か取り出して試験を行います。これを「母集団からサンプリングを行う」と言います。

今回の例では、「その日工場で製造したアルミ部品全ての強度試験結果＝母集団」で「試験用にアルミ部品を抜き出す＝サンプリング」、「試験用に取り出したアルミ部品＝サンプル」になります。

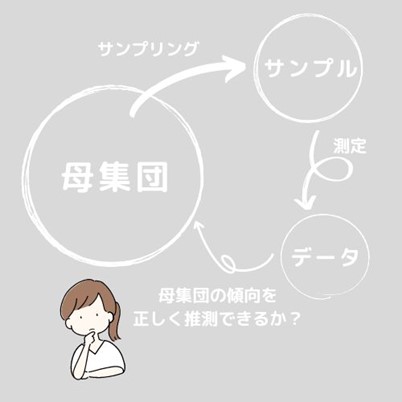
母集団・サンプル・データ

ばらつきとサンプリング

またサンプルには必ず「ばらつき」が含まれます。いくら同じ条件で製造を行っていて肉眼では同じように見えるアルミ部品でも、全く同じ強度にはなりません。

ばらつきの原因は、微妙な材料の違い、製造条件の違い、サンプリングの偏り、測定器のばらつきなど様々な要因が考えられます。したがってサンプリングしたデータで合否などを判断するときは、データのばらつきの影響が本当にないのかを検討する必要があります。

ばらつきの原因の1つであるサンプリングの偏りは完全に排除するのは難しいですが、できるだけ注意して行いましょう。十分に注意し偏りなくサンプリングすることを「ランダムサンプリング」と言います。
さきほどのアルミ部品の例で言うと、サンプリングした10個のアルミ部品が、朝のうちにまとめてサンプリングしたものだとすると、これはランダムサンプリングとは言えません。サンプリングした後に何か変動があったときにその後の製品の傾向がサンプルには現れないためです。

以上から、問題文は「あるアルミ部品製造工場でその日に生産されたアルミ部品の強度の傾向を知りたい。生産されたアルミ部品のうち10個を偏りなく取り出して試験した結果から、全体の傾向を知るにはどうしたらいいか？」という意味であることが分かります。

選択肢と解答・解説

次に選択肢と解答の解説をします。

a. 平均値xだけを求める
→平均値の求め方は割愛しますが、今回の例では合計845÷10サンプル＝84.5　となります。平均値は母集団の傾向を知る大切な尺度ではありますが、それだけではばらつきの傾向が読み取れません。このため母集団の傾向を知るには不十分なため不正解です。
b. 中心値（メディアンx）だけを調べる。
→中心値とはデータを大きさ順に並べたとき真ん中にくるデータです。データ数が奇数個の場合は真ん中のデータ、偶数個の場合は真ん中の2つのデータの平均となります。(今回の場合は(90+85)÷2＝87.5)
中心値も平均値と同様、ばらつきの傾向が読み取れないため、母集団の傾向を知るには不十分なので不正解です。
c. 範囲Rだけを調べる。
→範囲はデータの最大値と最小値の差(100-60＝40)で、ばらつきを表す尺度の1つです。範囲だけではデータの平均的(中心)傾向を表せていないので、不正解です。
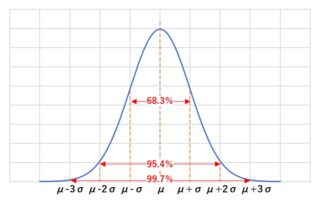
またばらつきを表す尺度には、他に平方和S、標準偏差σ、分散Vなどがありますが、QC検定4級では出題範囲ではありません。
d. ランダムサンプリングを行ったので、データには全くばらつきがない。
→問題文についての解説の通り、ランダムサンプリングをするよう努めなければいけませんが、全くばらつきなくサンプリングを行うのは難しいです。このためaは不正解です。
e. データは必ずばらつくので、平均的（中心）傾向とばらつき傾向の両面を検討する。
→eが正解になります。平均値xや中心値xのような平均的（中心）傾向と範囲Rのようなばらつき傾向の両面がないと母集団の性質は語ることができません。