母集団と標本の違いをわかりやすく解説 ― 不偏分散・母分散で理解する統計量の本質

当連載コラムの第3回「多変量解析に必要な統計基礎を解説!」では統計解析の基礎となるデータのばらつきと正規分布、標準偏差、分散の関係を調べました。
実は分散を表す言葉・定義式は複数存在し、それぞれの意味と使い分けを混同してしまうことがよくあります。
目次
1. 母分散と不偏分散(標本分散)とは
高校の数学で習う分散は「分散(variance)」と呼ばれ、多くの方がご存じの以下の式で定義されます。「母分散(population variance)」とも呼ばれます。
![]() (式1)
(式1)
ここで、σ²、N、Xi、μは、母分散、母集団のデータ数、各データの値、母集団のデータの平均値を表します。
ところが大学の統計学で学ぶ分散は「不偏分散(unbiased variance)」が主となり、以下の式で定義されます。
「標本分散(sample variance)」とも呼ばれます。
![]() (式2)
(式2)
ここで、s²、n、Xi、![]() は、不偏分散、標本のデータ数、各データの値、標本のデータの平均値を表します。
は、不偏分散、標本のデータ数、各データの値、標本のデータの平均値を表します。
分子の偏差平方和は同じと考えてよいので、上記の2つの定義の式の違いは分母がnであるか、n-1であるか、です。(式1)の名称には「母分散」の「母」という言葉が入っていますし、(式2)の名称には「標本分散」の「標本」という言葉が入っています。2つの式の違いを理解するためには、記述統計学のもっとも基本的な概念である「母集団(population)」と「標本(sample)」の違いを理解する必要があります。
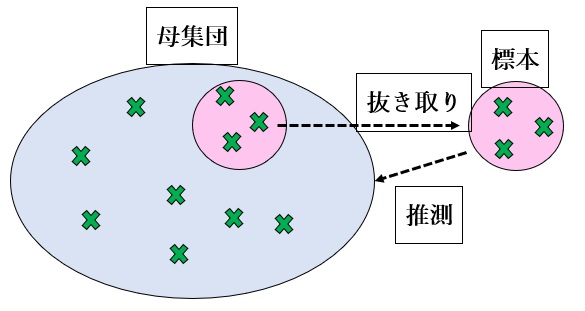
【図1 「母集団」と「標本」の違い】
2. 母分散と不偏分散の違いの由来
例えば、ある工場で生産している製品の重量を管理していると想定します。
また、上図で×印が個々の製品の重量を表しているものとします。
「母集団」とは、すべての製品の重量の集合を指します。毎日何十万個もの製品を生産している場合、母集団はそれらすべての製品重量データの集合になります。日々の品質管理では、膨大な数のすべての製品の重量を量る代わりに、母集団の一部、すなわち製品の何個かを抜き取り重量を量ります。その抜き取った製品の重量の集合を「標本」と呼びます。したがって統計処理する対象のデータ集合が異なります。
自由度から考える「n−1」という分母の意味
(式1)と(式2)でなぜ n と n-1 の違いが出てくるのかはいくつかの説明方法があります。
数式を使ってより厳密に期待値を評価する方法もあるのですが、煩雑な式になりますので、ここではよく利用される「自由度(degree of freedom)」という考え方を使って理解してみましょう。
本当に推測したいのは抜き取り方に依存する標本の分散でなく、データの全貌を表現する母集団の分散(母分散)のはずです。
母集団の代わりに抜き取った標本データで代用する場合、母集団の真の平均値μがわかっている場合に、(式1)の分散の式を使ってデータの偏差平方和をデータ数nで割って評価することに大きな問題はありません。ところが母集団の真の平均値はわからないのが通常のケースですから、標本の平均値で代用することになります。
分散の計算式にはXiのデータ数n個と平均値![]() のデータ数1個を合計した(n+1)個の数値を使いますが、平均値はn個のデータを使って計算されます。別の言い方をすると、もし任意の(n-1)個のデータおよび平均値がわかれば、平均値の値を満足するように残り1個のデータは自動的に決まってしまいます。
のデータ数1個を合計した(n+1)個の数値を使いますが、平均値はn個のデータを使って計算されます。別の言い方をすると、もし任意の(n-1)個のデータおよび平均値がわかれば、平均値の値を満足するように残り1個のデータは自動的に決まってしまいます。
このような状況を自由度が(n-1)であるという言い方をします。任意に決めることができるデータの数(自由度)1減ったと言えます。
実質的に自由に決めることができるデータの個数が(n-1)個になったので、それを反映して分母を(n-1)とした計算式を「不偏分散」あるいは「標本分散」と呼んで母集団の推定値としているわけです。
nの値が多い場合は分母がnでも(n-1)でも(式1)と(式2)の分散の値はあまり変わりませんが、nの値が小さい時は違いが出てきます。
自分の手で分散を計算する機会は少ないでしょうが、ソフトを使って計算する時はどちらの式を使って計算しているのかに注意しましょう。ExcelではVAR.P関数が母分散、VAR.S関数が不偏分散の計算に対応しています。
結論としては、母集団の真の平均値がわかっている場合は「母分散」の式を、わかっていない場合は「不偏分散」の式を使うようにしましょう。
3. 母集団と標本の統計量の比較
以上の議論をもとに母集団と標本の統計量を以下に比較してみます。
(1)母集団の統計量
まず、母集団の統計量です。
母集団の平均(母平均):
![]()
母集団の分散(母分散):
![]()
母集団の標準偏差(母標準偏差):
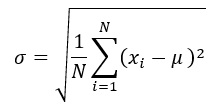
ここで、σ²、N、Xi、μは母分散、母集団のデータ数、各データの値、母集団のデータの平均値を表します。
いずれの式も分母はNで、統計量はすべて母集団の全データを用いて計算しますので標本の抜き取りの仕方に影響されません。
(2)標本の統計量
次に標本の統計量です。
標本の平均(標本平均):
![]()
標本の分散(標本分散):
![]()
標本の標準偏差(標本標準偏差):
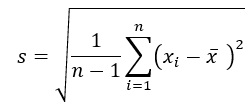
ここで、s²、n、Xi、![]() は不偏分散、標本のデータ数、各データの値、標本のデータの平均値を表します。
は不偏分散、標本のデータ数、各データの値、標本のデータの平均値を表します。
平均の式の分母はnですが、分散と標準偏差の式の分母は(n-1)です。母平均・母分散の値と異なり、標本平均・標本分散の値はどの製品を抜き取ったかによって変わってくることを覚えておきましょう。もちろん抜き取り数が全データ数(母集団の数)に近づくにしたがって母平均・母分散の値に近づきますから、抜き取り数が多いほど真の統計量を表現していることになるわけです。
4. おわりに
今回は統計の理論を勉強し始めた時にわかりにくい母集団と標本の違いを説明しました。
ソフトを使って分散を計算する時にはどちらの定義式(EXCELの場合はVAR.P関数とVAR.S関数)を使っているか意識するようにしましょう。
(アイアール技術者教育研究所 A・T)









](https://engineer-education.com/wp/wp-content/uploads/2022/09/experimental-design_statistics_1-150x150.png)
![英語版「実験計画法入門[統計編]」/Introduction to Design of Experiments Method – Statistics Edition(eラーニング)](https://engineer-education.com/wp/wp-content/uploads/2023/09/img-design-experiments-method_english-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2024/07/orthogonal-array-experiment-flow-150x150.png)
































