多変量解析の基本「回帰分析」を初心者向けに解説！Excelでの分析手順例も紹介
「多変量解析」の代表格は回帰分析で、企業の実務の現場で長年利用されてきました。
一方AIおよびデータサイエンスが今後の社会を大きく変革していくことが予想される時代が到来し、多変量解析は機械学習の応用分野の一つとして、回帰分析以外の手法の多様化・高度化あるいは応用分野の拡大がどんどん進んでいます。
この連載では多変量解析の基礎となる考え方・用語について、初心者の方にもわかりやすく解説していきます。
第1回目は伝統的な回帰分析を例として取り上げ、多変量解析の初歩的な手順および知っておかなければならない用語を中心に説明します。
１．回帰分析とは？
ほとんどの皆さんがご存じの回帰分析は、どのような計算原理に基づいているのかを知らなくても、例えば以下の手順で簡単に分析を実行することができます。
Excelでの分析手順の例
この例では高度なソフトを使わなくてもExcelだけで簡単に作図し有用な統計量を計算することができます。
まず8組のデータ(青●)をExcelに入力した後、挿入タブの「散布図」を選択して以下のグラフを描きます。
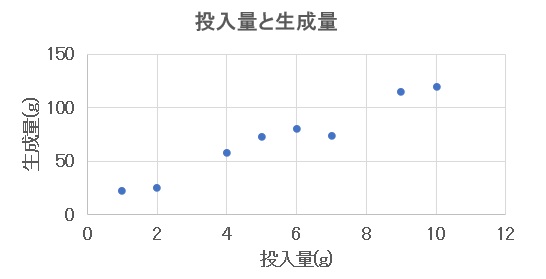
【図1 散布図(1) 】
次にExcel上のデータを左クリックして選択した後、さらに右クリックして「近似曲線の追加」を選択すると以下の画面が表示されます。その後、その画面上で「グラフに数式を表示する」と「グラフにR-2乗値を表示する」の2項目にチェックを入れます。
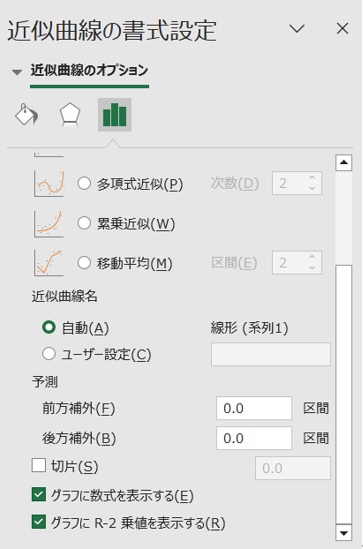
【図2 Excelの”近似曲線の書式設定”】
すると以下のように分析結果が重ねて表示されます。
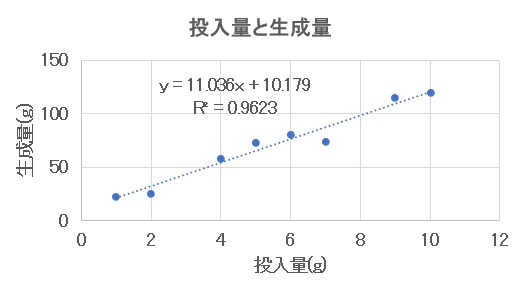
【図3 散布図(2) 】
回帰式と決定係数
この例では、生産プロセスで一つの原料の投入量を変えながら最終生成物の生成量を測定したとしています。
図1では8組のデータをプロットしていますが、このようなグラフには「散布図」という名前が付けられています。この例では変数が2つで、投入量は現象の原因となる変数で「説明変数」と呼ばれ、生成量は現象の結果となる変数で「目的変数」と呼ばれています。
図3中に記入されている投入量(x)と生成量(y)の数式は8組のデータをもとに線形な関係式を計算した結果です。
この関係式を求める解析が「回帰分析」と呼ばれる手法で、求められる関係式は「回帰式」と呼ばれます。この例では直線（図中の破線）で回帰していますが、任意の曲線で回帰して構いません。回帰式の直線は図中の破線で示されています。
さらに回帰直線がデータをどれだけうまく説明できるか評価するために、図中にある「R2(決定係数)」を計算することが一般的です。R2は0～1の範囲を取ります。「相関係数」の言葉をご存じの方にとっては、相関係数を二乗した値が決定係数になるという言い方ができます。
「データを説明できる（できない）」の考え方
R² = 1 の場合
R² = 1の時、回帰モデルがすべてのデータを完璧に説明でき、すべてのデータ点が回帰直線上に位置していることを示します。以下の図のようなケースです。
データ(青●)がすべて一本の直線（破線）上にあり、すべてのデータにつき横軸の値がわかれば回帰直線の式から縦軸の値が正確にわかります。この例ではたまたま傾きが負で原点を通っていますが、傾きは正でも構いませんし、原点を通っていなくても構いません。
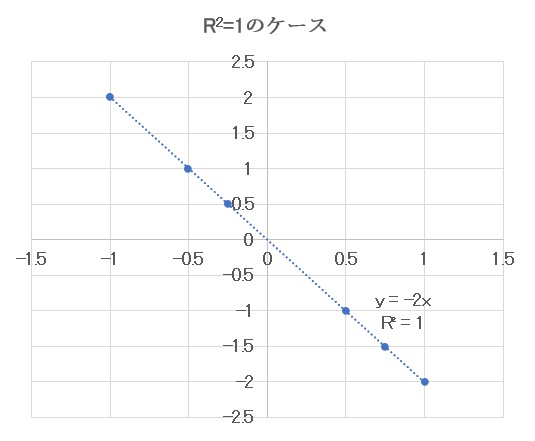
【図4 R²=1の回帰モデル】
R² = 0 の場合
R² = 0の時、回帰モデルがデータを全く説明できず、回帰直線が実際のデータとは無関係であることを示します。以下の図のようなケースです。
この例では半径1の円周上に等間隔で並んでいる8点(青●)をデータととしています。Excelで計算される回帰直線（破線）はy=0（x軸上の直線）となっていますが、このケースでは例えば回帰式はx=0としてもy=xでとしても同じR² = 0となり、データをもっともよく再現できる回帰式を1本に決めることができません。したがって回帰直線を求めてデータを再現あるいは予測することができなくなります。R² = 0でなくてもR² の値が小さくなるに従い、一本の回帰直線を使って予測することが無理になってくることはご理解いただけると思います。
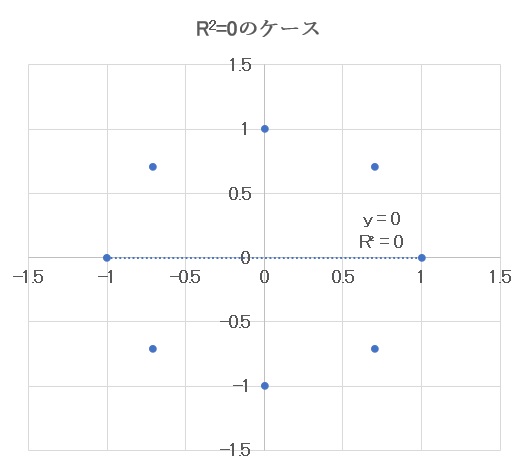
【図5 R²=0の回帰モデル】
さて、例えば「R²=0.95であれば回帰直線はデータを95%説明できる」というような言い方をします。
さきほどの投入量と生成量のケースに戻ると、決定係数はR²=0.9623なので、現象を説明できるかなり良いモデルであると評価することができ、未知の投入量に対応する生成量を精度よく予測することができます。例えば投入量を3(g)とか8(g)に変更した場合に、生成量がどの程度になるかを良い精度で予測できるだろうと考えます。
ただし、予測したい投入量の値が測定した投入量データの最小値より大きく最大値より小さい場合（「内挿」と呼ばれるケース）では予測精度は良いと考えられますが、投入量が最小値より小さいか最大値より大きい場合（「外挿」と呼ばれる）には一般に精度が悪くなりそうだということはご理解いただけると思います。
２．回帰分析の注意点
最後に、回帰分析の場合は理論を知らなくてもExcelですぐに計算できてしまうので、実際に利用する上での注意点を挙げておきます。
データ数が多いケースとデータ数が少ないケースの決定係数の大小を単純に比較して精度の良し悪しを決めるのは危険です。データ数が多いケースは、データ数が少ないケースに比べて決定係数の値が大きくなる傾向があると言われています。
例えばデータ数が少ない場合には、「外れ値」と呼ばれる、回帰直線から大きく外れたデータが存在した場合に決定係数が小さくなる要因となります。
一方、データ数が多い場合は他のデータが大勢を決めるため、外れ値があったとしても決定係数への影響は小さくなります。散布図を見て明らかに外れ値が存在する場合は、そのデータを削除して分析（「データクレンジング」と呼ばれる）することも予測精度を向上させるための重要な手段となります。
多変数を取り扱う場合はさらに新たな問題が発生します。
そのような課題を含めて、どのような理論で回帰分析を計算するのかについては、数式を交えて回帰分析の回で改めてご説明する予定です。
（アイアール技術者教育研究所 A・T)
